докажите что средняя линия трапеции параллельна основаниям

Средняя линия трапеции. 8-й класс

Разделы: Математика

Класс: 8

1) познакомить учащихся с понятием средней линии трапеции, рассмотреть её свойства и доказать их;

2) научить строить среднюю линию трапеции;

3) развивать умение учащихся использовать определение средней линии трапеции и свойства средней линии трапеции при решении задач;

4) продолжать формировать у учащихся умение говорить грамотно, используя необходимые математические термины; доказывать свою точку зрения;

5) развивать логическое мышление, память, внимание.

1. Проверка домашнего задания происходит в течение урока. Домашнее задание было устным, вспомнить:

а) определение трапеции; виды трапеций;

б) определение средней линии треугольника;

в) свойство средней линии треугольника;

г) признак средней линии треугольника.

2. Изучение нового материала.

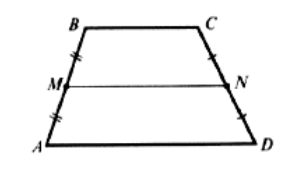
а) На доске изображена трапеция ABCD.

б) Учитель предлагает вспомнить определение трапеции. На каждой парте имеется схема-подсказка, помогающая вспомнить основные понятия в теме “Трапеция” (см. Приложение 1). Приложение 1 выдаётся на каждую парту.

Ученики изображают трапецию ABCD в тетради.

в) Учитель предлагает вспомнить, в какой теме встречалось понятие средней линии (“Средняя линия треугольника”). Учащиеся вспоминают определение средней линии треугольника и её свойство.

г) Далее, ребята вместе с учителем проводят аналогию между треугольником и трапецией, выясняют может ли существовать средняя линия в трапеции, и если да, то какими возможными свойствами она может обладать.

д) Записывают определение средней линии трапеции, изображая её в тетради.

Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Свойство средней линии трапеции на данном этапе остаётся не доказанным, поэтому следующий этап урока предполагает работу над доказательством свойства средней линии трапеции.

Теорема. Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Дано: ABCD – трапеция,

MN – средняя линия ABCD

Доказать, что:

2. MN = (AD + BC).

Можно выписать некоторые следствия, вытекающие из условия теоремы:

AM = MB, CN = ND, BC || AD.

На основании только перечисленных свойств доказать требуемое невозможно. Система вопросов и упражнений должна подвести учащихся к желанию связать среднюю линию трапеции со средней линией какого-нибудь треугольника, свойства которой они уже знают. Если предложений не последует, то можно задать вопрос: как построить треугольник, для которого отрезок MN являлся бы средней линией?

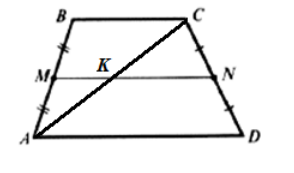
Запишем дополнительное построение для одного из случаев.

Проведём прямую BN, пересекающую продолжение стороны AD в точке K.

Появляется дополнительные элементы – треугольники: ABD, BNM, DNK, BCN. Если мы докажем, что BN = NK, то это будет означать, что MN – средняя линия ABD, а дальше можно будет воспользоваться свойством средней линии треугольника и доказать необходимое.

а) CNB =DNK (свойство вертикальных углов);

б) BCN = NDK (свойство внутренних накрест лежащих углов);

в) CN = ND (по следствию из условия теоремы).

Что и требовалось доказать.

Доказательство можно провести на уроке устно, а дома восстановить и записать в тетради (на усмотрение учителя).

Необходимо сказать и о других возможных способ доказательства этой теоремы:

1. Провести одну из диагоналей трапеции и использовать признак и свойство средней линии треугольника.

2. Провести CF || BA и рассмотреть параллелограмм ABCF и DCF.

3. Провести EF || BA и рассмотреть равенство FND и ENC.

ж) На этом этапе задаётся домашнее задание: п. 84, учебник под ред. Атанасяна Л.С. (доказательство свойства средней линии трапеции векторным способом), записать в тетради.

з) Решаем задачи на использование определения и свойства средней линии трапеции по готовым чертежам (см. Приложение 2). Приложение 2 выдаётся каждому учащемуся, и решение задач оформляется на этом же листе в краткой форме.

Источник

Что такое средняя линия трапеции

В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.

Определение средней линии трапеции

Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.

Свойства средней линии трапеции

Свойство 1

Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.

Свойство 2

Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.

Свойство 3

Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):

Признак средней линии трапеции

Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.

Вторая средняя линия

Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.

Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.

Пример задачи

Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.

Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b) /₂ ⋅ h

В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b) /₂.

Источник

Средняя линия трапеции

Вы будете перенаправлены на Автор24

Понятие средней линии трапеции

Для начала вспомним, какую фигуру называют трапецией.

Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны.

Теорема о средней линии трапеции

Теперь введем теорему о средней линии трапеции и докажем её векторным методом.

Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.

Рисунок 1. Средняя линия трапеции

Сложим два последних равенства, получим

Теорема доказана.

Примеры задач на понятие средней линии трапеции

Решение.

Сумма боковых сторон равна

Значит, по теореме 1, получаем

Готовые работы на аналогичную тему

Решение.

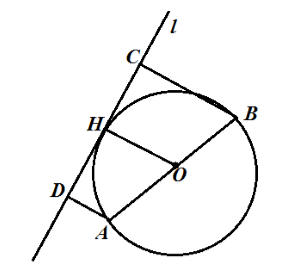
\[d=2OH=2\cdot 7\ см=14\ см.\]

Доказать, что средняя линия трапеции проходит через середину произвольной диагонали данной трапеции.

Доказательство.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 01 04 2021

Источник

Методика работы с теоремой о средней линии трапеции

Методика работы с теоремой о средней линии трапеции (геометрия 8 класс)

Основные этапы работы с теоремой

Мотивация изучения теоремы и раскрытие ее содержания (усмотрение геометрического факта и формулировки теоремы).

Работа над структурой теоремы.

Построение чертежа и краткая запись содержания теоремы.

Поиск доказательства, доказательство и его запись.

1-й этап. Мотивация изучения теоремы и раскрытие ее содержания (усмотрение геометрического факта и формулировки теоремы).

Мотивация необходимости изучения данной теоремы: решение небольшой практической задачи, проблемная ситуация.

Теорема: « C редняя линия трапеции параллельна основаниям и равна их полусумме».

Теорема сформулирована в категорической форме.

Сформулируем ее в условной форме, выделив явно разъяснительную часть: в любой трапеции, если есть ее средняя линия, то она параллельна основаниям и равна их полусумме.

2-й этап . Работа над структурой.

Структура теоремы такова:

Разъяснительная часть – в любой трапеции;

Условие – отрезок есть средняя линия трапеции;

Заключение – 1) отрезок параллелен основаниям; 2) отрезок равен полусумме оснований.

Теорема содержит два заключения

3-й этап. Построение чертежа и краткая запись содержания теоремы.

MN – средняя линия трапеции

4- й этап . Поиск доказательства, доказательство и его запись.

Возможно дедуктивное введение теоремы и синтетический способ ее доказательства.

Однако активизации познавательной деятельности учащихся будет способствовать метод эксперимента. Свойства средней линии трапеции можно «открыть» параллельно с процессом построения средней линии в произвольных трапециях. Учащимся предлагается:

Сравнить визуально взаимное расположение средней линии и оснований трапеции;

Построить отрезок, длина которого равна сумме длин оснований трапеции. Сколько раз средняя линия укладывается на этом отрезке?

На основе выполнения задания выдвигается гипотеза о том, что средняя линия параллельна основаниям трапеции и равна ее половине.

Далее формулируется теорема, делается чертеж, записывается, что дано и требуется доказать.

Анализ. Поиск путей доказательства:

Дайте определение трапеции. Какие прямые в нашем случае параллельны, как они называются? Требуется доказать, что средняя линия параллельна двум основаниям, то есть двум параллельным прямым. Как упростить путь доказательства этого факта? Достаточно доказать параллельность одному из оснований.

Чем можно воспользоваться? Для какой фигуры, кроме трапеции определено понятие средней линии? Нельзя ли использовать теорему о средней линии треугольника для доказательства? Можно ли отыскать или провести дополнительные построения, чтобы получить треугольник, средняя линия которого совпадает со средней линией трапеции?

Синтез . Составление плана доказательства.

Для доказательства из вершины B через точку N проведём прямую BN до пересечения этой прямой с продолжением основания AD в точке B _{1 .}

1=2 (как вертикальные); 3=4 (как накрест лежащие при пересечении параллельных прямых BC и А B ₁ секущей CD ); CN = ND (по построению)

Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

Дано: ABCD – трапеция;

MN – средняя линия трапеции;

Доказать: MN || AD; MN || BC;

Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

Дано: ABCD – трапеция;

MN – средняя линия трапеции;

Теорема : средняя линия трапеции параллельна основаниям и равна их полусумме.

Дано: ABCD – трапеция;

MN – средняя линия трапеции;

Доказать: MN || AD; MN || BC;

Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

Дано: ABCD – трапеция;

MN – средняя линия трапеции;

Доказать: MN || AD; MN || BC;

Теорема: средняя линия трапеции параллельна основаниям и равна их полусумме.

Дано: ABCD – трапеция;

MN – средняя линия трапеции;

Источник

Доказательство средней линии трапеции

Средняя линия трапеции.

Средняя линия трапеции равна полусумме оснований

http*://dcs.isa*.ru/www/vladimirv/Geometry/dshar/sco_6.2.3/sco_6.2.3.html
СМОТРИ с рисунками подробно (звездочки в ссылке убрать)

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.
Пусть отрезок РК – средняя линия трапеции ABCD и прямые ВР и AD пересекаются в точке Т.

Треугольники ВСР и PDT равны (так как PC=PD, ÐВРС=ÐDPT, ÐВСР=ÐPDT). Поэтому BC=DT, BP=PT и AT=AD+DT. Отсюда средняя линия данной трапеции является средней линией и треугольника АВТ. По теореме средней линии треугольника PK||AT и PK=AT×1/2. Значит, PK||AD и PK=(BC+AD)/2.

http*://dcs.isa*.ru/www/vladimirv/Geometry/dshar/sco_6.2.3/sco_6.2.3.html
СМОТРИ с рисунками подробно (звездочки в ссылке убрать)

Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Доказательство.
Пусть отрезок РК – средняя линия трапеции ABCD и прямые ВР и AD пересекаются в точке Т.

Треугольники ВСР и PDT равны (так как PC=PD, ÐВРС=ÐDPT, ÐВСР=ÐPDT). Поэтому BC=DT, BP=PT и AT=AD+DT. Отсюда средняя линия данной трапеции является средней линией и треугольника АВТ. По теореме средней линии треугольника PK||AT и PK=AT×1/2. Значит, PK||AD и PK=(BC+AD)/2.

Математика Докажите, что средняя линия трапеции параллельна основаниям и равна их полусумме.

Источник