докажите что средняя линия трапеции равна полусумме ее оснований
Средняя линия трапеции равна полусумме ее оснований
Здравствуйте!
Нужно доказать, что средняя линия трапеции равна полусумме ее оснований. Помогите, пожалуйста!
Спасибо!
Задание.
Доказать, что средняя линия трапеции равна полусумме ее оснований.
Доказательство.
Построим произвольную тр-цию KLMN.
Основаниями тр-ции будут стороны KN и LM.
Отметим точками Н и Р середины боковых сторон KL и MN тр-ции соответственно.
Проведем через точки Н и Р ср. линию тр-ции.
Необходимо доказать, что ср. линия НР тр-ции равна половине суммы оснований KN и LM:

По св-ву ср. линии тр-ции, она проходит параллельно к нижн. и верхн. основаниям тр-ции.
Проведем диагональ тр-ции LN и обозначим точку пересечения диагонали со ср. линией Q.
Диагональ тр-ции делит ее на два треуг-ника — KLN и MLN.
Рассмотрим треуг-ник KLN.
Отрезок HQ будет являться ср. линией этого треуг-ника, так как точка Н — середина стороны KL и HQ парал-но KN. По св-ву ср. линии треуг-ника выразим ее длину через основание KN:
Рассмотрим треуг-ник MLN.
Отрезок РQ будет являться ср. линией этого треуг-ника, так как точка Р — середина стороны MN и PQ парал-но LM. По св-ву ср. линии треуг-ника выразим ее длину через основание LM:
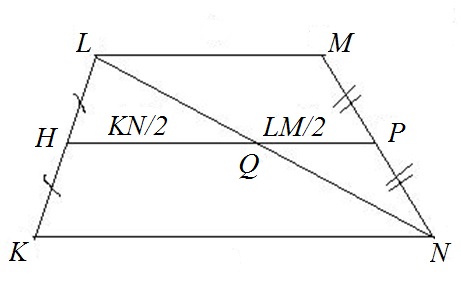
Ср. линия тр-ции KLMN состоит из двух ср. линий треуг-ников KLN и MLN:
Подставим найденные значения ср. линий треуг-ников:
В результате получаем, что ср. линия тр-ции равна половине суммы ее оснований.
Доказательство завершено.
Средняя линия трапеции. 8-й класс
Разделы: Математика
Класс: 8
1) познакомить учащихся с понятием средней линии трапеции, рассмотреть её свойства и доказать их;
2) научить строить среднюю линию трапеции;
3) развивать умение учащихся использовать определение средней линии трапеции и свойства средней линии трапеции при решении задач;
4) продолжать формировать у учащихся умение говорить грамотно, используя необходимые математические термины; доказывать свою точку зрения;
5) развивать логическое мышление, память, внимание.
1. Проверка домашнего задания происходит в течение урока. Домашнее задание было устным, вспомнить:
а) определение трапеции; виды трапеций;
б) определение средней линии треугольника;
в) свойство средней линии треугольника;
г) признак средней линии треугольника.
2. Изучение нового материала.
а) На доске изображена трапеция ABCD.
б) Учитель предлагает вспомнить определение трапеции. На каждой парте имеется схема-подсказка, помогающая вспомнить основные понятия в теме “Трапеция” (см. Приложение 1). Приложение 1 выдаётся на каждую парту.
Ученики изображают трапецию ABCD в тетради.
в) Учитель предлагает вспомнить, в какой теме встречалось понятие средней линии (“Средняя линия треугольника”). Учащиеся вспоминают определение средней линии треугольника и её свойство.
г) Далее, ребята вместе с учителем проводят аналогию между треугольником и трапецией, выясняют может ли существовать средняя линия в трапеции, и если да, то какими возможными свойствами она может обладать.
д) Записывают определение средней линии трапеции, изображая её в тетради.
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.
Свойство средней линии трапеции на данном этапе остаётся не доказанным, поэтому следующий этап урока предполагает работу над доказательством свойства средней линии трапеции.
Теорема. Средняя линия трапеции параллельна её основаниям и равна их полусумме.
Дано: ABCD – трапеция,
MN – средняя линия ABCD
Доказать, что:
2. MN = 
Можно выписать некоторые следствия, вытекающие из условия теоремы:
AM = MB, CN = ND, BC || AD.
На основании только перечисленных свойств доказать требуемое невозможно. Система вопросов и упражнений должна подвести учащихся к желанию связать среднюю линию трапеции со средней линией какого-нибудь треугольника, свойства которой они уже знают. Если предложений не последует, то можно задать вопрос: как построить треугольник, для которого отрезок MN являлся бы средней линией?
Запишем дополнительное построение для одного из случаев.
Проведём прямую BN, пересекающую продолжение стороны AD в точке K.
Появляется дополнительные элементы – треугольники: ABD, BNM, DNK, BCN. Если мы докажем, что BN = NK, то это будет означать, что MN – средняя линия 
а) 

б) 

в) CN = ND (по следствию из условия теоремы).
Что и требовалось доказать.
Доказательство можно провести на уроке устно, а дома восстановить и записать в тетради (на усмотрение учителя).
Необходимо сказать и о других возможных способ доказательства этой теоремы:
1. Провести одну из диагоналей трапеции и использовать признак и свойство средней линии треугольника.
2. Провести CF || BA и рассмотреть параллелограмм ABCF и 
3. Провести EF || BA и рассмотреть равенство 

ж) На этом этапе задаётся домашнее задание: п. 84, учебник под ред. Атанасяна Л.С. (доказательство свойства средней линии трапеции векторным способом), записать в тетради.
з) Решаем задачи на использование определения и свойства средней линии трапеции по готовым чертежам (см. Приложение 2). Приложение 2 выдаётся каждому учащемуся, и решение задач оформляется на этом же листе в краткой форме.
Что такое средняя линия трапеции
В данной публикации мы рассмотрим определение, свойства и признак средней линии трапеции, а также разберем пример решения задачи для лучшего понимания изложенного материала.
Определение средней линии трапеции
Отрезок, соединяющий середины боковых сторон трапеции, называется ее средней линией.
Свойства средней линии трапеции
Свойство 1
Средняя линия трапеции параллельна ее основаниям и равняется их полусумме.
Свойство 2
Средняя линия трапеции делит пополам любой отрезок, концы которого лежат на основаниях данной трапеции.
Свойство 3
Средняя линия трапеции делит ее на две другие трапеции, площади которых соотносятся следующим образом (см. первый чертеж публикации):
Признак средней линии трапеции
Если отрезок, выходящий из середины боковой стороны трапеции, пересекает ее вторую боковую сторону и, при этом, параллелен основаниям фигуры, то он является средней линией этой трапеции.
Вторая средняя линия
Иногда дополнительно выделяют вторую среднюю линию трапеции – отрезок, соединяющий середины ее оснований. При этом следует помнить, что к ней не применимы Свойства 1-3 и Признак, рассмотренные выше.
Вторая средняя линия равнобедренной трапеции одновременно является ее высотой.
Пример задачи
Средняя линия трапеции равняется 25 см, а ее высота – 7 см. Найдите площадь фигуры.
Как мы знаем, площадь трапеции равняется полусумме оснований, умноженной на высоту h: S = (a+b) /2 ⋅ h
В данном случае полусумма оснований – это и есть средняя линия. Обозначим ее буквой m. То есть m = (a+b) /2.
Доказательство средней линии трапеции
Средняя линия трапеции.
Средняя линия трапеции равна полусумме оснований
http*://dcs.isa*.ru/www/vladimirv/Geometry/dshar/sco_6.2.3/sco_6.2.3.html
СМОТРИ с рисунками подробно (звездочки в ссылке убрать)
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть отрезок РК – средняя линия трапеции ABCD и прямые ВР и AD пересекаются в точке Т.
Треугольники ВСР и PDT равны (так как PC=PD, ÐВРС=ÐDPT, ÐВСР=ÐPDT). Поэтому BC=DT, BP=PT и AT=AD+DT. Отсюда средняя линия данной трапеции является средней линией и треугольника АВТ. По теореме средней линии треугольника PK||AT и PK=AT×1/2. Значит, PK||AD и PK=(BC+AD)/2.
http*://dcs.isa*.ru/www/vladimirv/Geometry/dshar/sco_6.2.3/sco_6.2.3.html
СМОТРИ с рисунками подробно (звездочки в ссылке убрать)
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.
Доказательство.
Пусть отрезок РК – средняя линия трапеции ABCD и прямые ВР и AD пересекаются в точке Т.
Треугольники ВСР и PDT равны (так как PC=PD, ÐВРС=ÐDPT, ÐВСР=ÐPDT). Поэтому BC=DT, BP=PT и AT=AD+DT. Отсюда средняя линия данной трапеции является средней линией и треугольника АВТ. По теореме средней линии треугольника PK||AT и PK=AT×1/2. Значит, PK||AD и PK=(BC+AD)/2.
Математика Докажите, что средняя линия трапеции параллельна основаниям и равна их полусумме.
Изучение теоремы о средней линии и сравнение рассматриваемых учебников
Индивидуальное задание №1 по основаниям геометрии. Выполнил Куликов А. студент ПОМО132
Задание №3. Рассмотрим доказательство теоремы о средней линии трапеции
Учебник. Геометрия 7 – 9. Авторы: Л.С. Атанасян, В.Ф. Бутузов, С.Б.Кадомцев и др.
ТЕОРЕМА. Средняя линия трапеции параллельна основаниям и равно их полусумме.
ДОКАЗАТЕЛЬСТВО. Оно строится на векторной основе.
По правилу многоугольника получаем и
. Сложив эти равенства, получим:
Учебник. Геометрия 7 – 9. Автор: Погорелов А. В.
ТЕОРЕМА. Средняя линия трапеции параллельна основаниям и равна их полусумме.
ДОКАЗАТЕЛЬСТВО. Оно строится на основе дополнительного построения.
Пусть ABCD – данная трапеция. Проведём через вершину B и середину P боковой стороны CD прямую. Она пресекает прямую AD в некоторой точке Е.
Учебник. Геометрия 7 – 9 класс. Автор: Шарыгин И. Ф.
ТЕОРЕМА. Средняя линия трапеции параллельна основаниям трапеции и равна их полусумме
средней линии треугольника KP и PM параллельны
прямой, параллельной основаниям трапеции.
Задание №1. Аксиоматика школьных учебников
Основные понятия: точка, прямая, плоскость
Отношение измерения отрезка
Отношение равенства фигур
Взаимное расположение точек, прямых и плоскостей
Через любые две точки плоскости можно провести прямую линию и притом только одну
Любая точка, лежащая на прямой делит её на две полупрямых
Любая прямая плоскости делит её на две части – полуплоскости
Аксиомы измерения отрезков
Длина отрезка выражается положительным числом
Отношение длин любых двух отрезков не зависит от выбора единицы длины
Два отрезка называются равными, если при наложении совпадают их концы
Основные понятия: точка, прямая, плоскость
Отношение измерения отрезков и углов
Отношение откладывания отрезков и углов
Взаимное расположение точек, прямых и плоскостей
Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей
Через любые две точки можно провести прямую и только одну
Из трёх точек на прямой одна и только одна лежит между двумя другими
Прямая разбивает плоскость на две полуплоскости
Измерение отрезков и углов
Каждый отрезок имеет определённую длину, большую нуля.
Длина отрезка равна сумме частей, на которые он разбивается любой его точкой
Каждый угол имеет определённую градусную меру, большую нуля
Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами
На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один
Каков бы ни был треугольник, существует равный ему треугольник в заданном расположении относительно данной полупрямой
Основные понятия: точка, прямая, плоскость.
отношение «лежать между»
отношение равенства фигур
отношение измерения отрезков
Взаимное расположение точек, прямых и плоскостей
Каждой прямой принадлежит по крайней мере две точки
Имеются по крайней мере три точки, не лежащие на одной прямой
Через любые две точки проходит прямая и притом только одна
Из трёх точек прямой одна и только одна лежит между двумя другими
Аксиомы равенства фигур
Если при наложении совмещаются концы двух отрезков, то совмещаются и сами отрезки
На любом луче от его начала можно отложить отрезок, равный данному, и притом только один
От любого луча в данную полуплоскость можно отложить угол, равный данному неразвёрнутому углу, и притом только один
Любой угол hk можно совместить наложением с равным ему углом h 1 k 1 двумя способами:
Любая фигура равна самой себе
Аксиомы измерения отрезков
При выбранной единице измерения отрезков длина каждого отрезка выражается положительным числом
При выбранной единице измерения отрезков для любого положительного числа существует отрезок, длина которого выражается этим числом
Аксиома параллельности прямых
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-119785
Не нашли то что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Дума проведет расследование отклонения закона о школьных онлайн-ресурсах
Время чтения: 2 минуты
В России утвердили новый порядок формирования федерального перечня учебников
Время чтения: 1 минута
Минпросвещения планирует выделить «Профессионалитет» в отдельный уровень образования
Время чтения: 2 минуты
Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст
Время чтения: 1 минута
Путин призвал повышать уровень общей подготовки в колледжах
Время чтения: 1 минута
Путин поручил не считать выплаты за классное руководство в средней зарплате
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.





















