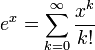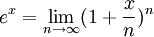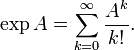Что такое экспонента определение
Экспоненциальная функция
Содержание
Определение
Экспоненциальная функция может быть определена различными эквивалентными способами. Например через ряд Тейлора:
Свойства
Экспонента от комплексного аргумента
От комплексного аргумента z = x + iy экспонента определяется следующим образом:
Вариации и обобщения
Аналогично экспонента может быть определена для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.
Матричная экспонента
Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:
Определённый таким образом ряд сходится для любого оператора A с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы A: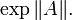 
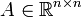
Следовательно, экспонента от матрицы 
всегда определена и сама является матрицей.
С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение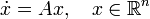 
с начальным условием x(0) = x0 имеет своим решением x(t) = exp(At)x0.
Обратная функция
Обратной функцией к экспоненциальной функции является натуральный логарифм.
Обозначается ln(x) :
См. также
Полезное
Смотреть что такое «Экспоненциальная функция» в других словарях:
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Большой Энциклопедический словарь
экспоненциальная функция — экспонента — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия Синонимы экспонента EN exponential function … Справочник технического переводчика
экспоненциальная функция — то же, что показательная функция. * * * ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ, то же, что показательная функция (см. ПОКАЗАТЕЛЬНАЯ ФУНКЦИЯ) … Энциклопедический словарь
экспоненциальная функция — eksponentinė funkcija statusas T sritis fizika atitikmenys: angl. exponential function vok. exponentielle Funktion, f rus. экспоненциальная функция, f pranc. fonction exponentielle, f … Fizikos terminų žodynas
Экспоненциальная функция — функция у = ex, то есть Показательная функция. Обозначается также y = exp х. Иногда Э. ф. называют и функцию у = ax при любом основании а > 0 … Большая советская энциклопедия
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — показа тельная функция, функция у=е х;обозначается также y = ехр х. Иногда Э. ф. наз. и функцию у = а х при любом основании а>0. БСЭ 3 … Математическая энциклопедия
ЭКСПОНЕНЦИАЛЬНАЯ ФУНКЦИЯ — то же, что показательная функция … Естествознание. Энциклопедический словарь
экспоненциальная — функция [ Словарь иностранных слов русского языка
экспонента
Смотреть что такое «экспонента» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
ЭКСПОНЕНТА — ЭКСПОНЕНТА, число, обозначающее степень, которое пишется в виде верхнего индекса справа от цифры или символа. Например, в выражении а4=(а3а3а3а) экспонентой является 4. Операции с экспонентами подчиняются некоторым законам. Например, З23З5=3(2+5) … Научно-технический энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
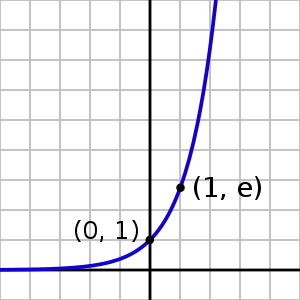
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
Значение слова «экспонент»
[От лат. exponens, exponentis — выставляющий напоказ]
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
ЭКСПОНЕ’НТ, а, м. [латин. exponens — выставляющий]. 1. Владелец экспоната, лицо, выставляющее что-н. на выставке (спец.). 2. Показатель степени (мат.).
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
экспоне́нт I
1. спец. участник выставки, выставляющий, демонстрирующий на ней что-либо ◆ Выставка не удалась, всё лезло врозь, экспоненты остались недовольны, недовольна осталась публика, недовольны газеты. В. Г. Короленко, «Павловские очерки», 1889—1890 г. (цитата из НКРЯ)
3. (в алгебре) показатель степени
4. (в семиотике) объект или знак, представляющий другой объект в иной системе
Делаем Карту слов лучше вместе
Привет! Меня зовут Лампобот, я компьютерная программа, которая помогает делать Карту слов. Я отлично умею считать, но пока плохо понимаю, как устроен ваш мир. Помоги мне разобраться!
Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова дегельминтизация (существительное):
Синонимы к слову «экспонент»
Предложения со словом «экспонент»
Цитаты из русской классики со словом «экспонент»
Сочетаемость слова «экспонент»
Понятия, связанные со словом «экспонент»
Общество осенних салонов, укороченное название Осенний салон (фр. Société du Salon d’automne, также Salon d’automne) — объединение деятелей искусства во Франции, основанное в 1903 году архитектором Францем Журденом в сотрудничестве с такими художниками, как Жорж Руо, Эдуар Вюйяр, Альбер Марке. В создании общества также принимали участие такие заслуженные мастера живописи, как Сезанн, Ренуар, Одилон Редон, Эжен Каррьер. Ренуар и Каррьер были избраны почётными президентами общества.
Отправить комментарий
Дополнительно
Предложения со словом «экспонент»
Этот показатель называется экспонентом, степенью или порядком числа.
Более того, за первые четыре отрезка времени рост экспоненты составляет только малую долю от линейного роста.
Но внутри шестого отрезка эти линии пересекаются, и ещё через два отрезка значения экспоненты становятся больше уже вдвое, а к десятому – в 10 раз.
ЭКСПОНЕНТА
Смотреть что такое «ЭКСПОНЕНТА» в других словарях:
ЭКСПОНЕНТА — (от лат. exponens показывающий) то же, что показательная кривая или (экспоненциальная) показательная функция … Большой Энциклопедический словарь
экспонента — сущ., кол во синонимов: 1 • кривая (56) Словарь синонимов ASIS. В.Н. Тришин. 2013 … Словарь синонимов
Экспонента — [exponent] показательная функция с основанием, равным иррациональному числу e, т.е. ex. Если показатель Э., еp(x) содержит сложные выражения, используется запись вида ep(x) = exp
ЭКСПОНЕНТА — (экспоненциальная функция) то же, что показательная функция с основанием, равным числу (см.), задаваемая формулой у = е1. Иногда обозначается ехр дг. Экспоненциальная кривая на плоскости является графиком экспоненты, которая встречается в… … Большая политехническая энциклопедия
Экспонента — У этого термина существуют и другие значения, см. Экспонента (значения). График экспоненты. Касательная в нуле у функции … Википедия
экспонента — (от лат. exponens показывающий), то же, что показательная кривая или (экспоненциальная) показательная функция. * * * ЭКСПОНЕНТА ЭКСПОНЕНТА (от лат. exponens показывающий), то же, что показательная кривая (см. ПОКАЗАТЕЛЬНАЯ КРИВАЯ) или… … Энциклопедический словарь
экспонента — eksponentė statusas T sritis automatika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Automatikos terminų žodynas
экспонента — eksponentė statusas T sritis fizika atitikmenys: angl. exponent vok. Exponente, f rus. экспонента, f pranc. exponentielle, f … Fizikos terminų žodynas
Для действительных чисел c и d функция формы также является экспоненциальной функцией, поскольку ее можно переписать как ж ( Икс ) знак равно а б c Икс + d <\ Displaystyle е (х) = ab ^ 
Экспоненциальную функцию иногда называют естественной экспоненциальной функцией, чтобы отличить ее от других экспоненциальных функций. Изучение любой экспоненциальной функции легко сводится к изучению естественной экспоненциальной функции, поскольку ж ( Икс ) знак равно е Икс <\ Displaystyle е (х) = е ^ <х>>
Как функции действительной переменной экспоненциальные функции однозначно характеризуются тем фактом, что скорость роста такой функции (то есть ее производной ) прямо пропорциональна значению функции. Константа пропорциональности этого отношения является натуральным логарифмом основания b :
Показательная функция удовлетворяет фундаментальному мультипликативному тождеству (которое также может быть расширено до комплексных показателей):
Аргументом экспоненциальной функции может быть любое действительное или комплексное число или даже математический объект совершенно другого типа (например, квадратная матрица ).
СОДЕРЖАНИЕ
Формальное определение
Посредством биномиальной теоремы и определения степенного ряда экспоненциальная функция также может быть определена как следующий предел:
Обзор
Производные и дифференциальные уравнения
Кроме того, для любой дифференцируемой функции f ( x ) по цепному правилу находим :
Непрерывные дроби для e x
или, применив замену z = Икс / у :
со специальным случаем для z = 2 :
Сложная плоскость
Как и в реальном случае, экспоненциальная функция может быть определена на комплексной плоскости в нескольких эквивалентных формах. Наиболее распространенное определение комплексной экспоненциальной функции аналогично определению степенного ряда для вещественных аргументов, где действительная переменная заменяется комплексной:
В качестве альтернативы, комплексная экспоненциальная функция может быть определена путем моделирования определения предела для реальных аргументов, но с заменой реальной переменной на сложную:
Определение комплексной экспоненциальной функции, в свою очередь, приводит к соответствующим определениям, расширяющим тригонометрические функции до сложных аргументов.
В частности, когда z = it ( t real), определение ряда дает разложение
В этом разложении преобразование членов в действительную и мнимую части оправдано абсолютной сходимостью ряда. Действительная и мнимая части приведенного выше выражения фактически соответствуют разложениям в ряды cos t и sin t соответственно.
Эти определения экспоненциальной и тригонометрической функций тривиально приводят к формуле Эйлера :
exp ( я z ) знак равно потому что z + я грех z для всех z ∈ C <\ Displaystyle \ ехр (iz) = \ соз z + я \ грех Z <\ текст <для всех>> z \ in \ mathbb .
Когда ее область определения расширяется от вещественной линии до комплексной плоскости, экспоненциальная функция сохраняет следующие свойства:
Затем мы можем определить более общее возведение в степень:
См. Отказ от тождества мощности и логарифма для получения дополнительной информации о проблемах с объединением степеней.