Что такое параллельные кривые

Параллельная кривая

Параллельная кривая плоской кривой — огибающая семейства окружностей равного радиуса, центры которых лежат на заданной кривой. Понятие параллельной кривой — обобщение понятия параллельной прямой на случай плоских кривых.

Для параметрически заданной кривой, параллельная кривая, проходящая на расстоянии от данной определяется уравнениями

, .

Или в векторной форме:

,

где матрица соответствует повороту вектора на 90° по часовой стрелке.

См. также

Внешние ссылки

Циклоида • Эпициклоида • Гипоциклоида • Трохоида (Удлинённая + Укороченная циклоида) • Эпитрохоида (Удлинённая + Укороченная эпициклоида • («Роза») • Гипотрохоида • Скорейшего спуска (Брахистохрона, дуга циклоиды)

Полезное

Смотреть что такое «Параллельная кривая» в других словарях:

Кривая Урысона — (далее кривая) наиболее общее (но не чрезмерно) определение кривой, введённое Урысоном в 1921. Это определение обобщает определение Кантора на произвольную размерность. Определение формулируется следующим образом: Кривой называется связное… … Википедия

Кривая Пеано — общее название для параметрических кривых, образ которых содержит квадрат (или, в более общем смысле, открытые области пространства) Содержание 1 Свойства 2 Примеры 3 Обобщения … Википедия

Кривая Леви — Кривая Леви фрактал. Предложен французским математиком П. Леви. Получается, если взять половину квадрата вида /, а затем каждую сторону заменить таким же фрагментом, и, повторяя эту операцию, в … Википедия

Кривая погони — при различных параметрах Кривая погони кривая, представляющая собой решение задачи о «погоне», которая ставится следующим образом. Пусть … Википедия

Кривая — У этого термина существуют и другие значения, см. Кривая (значения). Кривая или линия геометрическое понятие, определяемое в разных разделах геометрии различно. Содержание 1 Элементарная геометрия 2 … Википедия

Кривая Безье — Кривые Безье или Кривые Бернштейна Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен» … Википедия

Кривая Коха — В этой статье не хватает ссылок на источники информации. Информация должна быть проверяема, иначе она может быть поставлена под сомнение и удалена. Вы можете … Википедия

Кривая Минковского — Построение кривой Минковского Кривая Минковского классический геометрический фрактал, предложенный Минковским. Инициатором является отрезок, а генератором является ломаная из восьм … Википедия

Кривая постоянной ширины — Примеры … Википедия

Кривая Персея — 3 кривых: a=1, b=2, c=0; 0.8; 1 Кривая Персея плоская кривая 4 го порядка, задаваемая уравнением в декартовой системе координат … Википедия

Источник

Построение параллельных кривых в картографических веб-приложениях

В ходе работы над веб-картой в рамках проекта возникла задача отображения линий метрополитена на карте. Казалось бы, что в этом сложного? По сути — ничего, пока вам не требуется визуализировать различные маршруты, физически проходящие по одному месту. С такой ситуацией мы столкнулись при попытке отобразить линии амстердамского метрополитена.

Первая мысль, которая приходит в голову — это просто продублировать те сегменты, по которым проходит несколько маршрутов, немного сдвинув их друг относительно друга, меняя географические координаты. Однако в результате подобного действия мы получаем линии, которые на мелких масштабах сливаются друг с другом, а на крупных, наоборот, разлетаются в разные стороны, то есть, глядя на подобную карту, невозможно понять, что указанные маршруты физически проходят по одному месту.

Более правильный способ заключается в том, что сдвиг линий относительно друг друга должен задаваться в пикселах с учётом толщины линий. Приблизительный порядок действий должен быть следующим:

Вычисление координат сегмента, сдвинутого относительно базового на определённое расстояние по сути является задачей нахождения параллельной кривой.

Поскольку в веб-карте проекта «Метро для всех» используется картографическая библиотека Leaflet, то было решено попробовать найти какой-нибудь плагин для построения параллельных кривых. И такой плагин нашёлся — Leaflet.PolylineOffset, пример.

На тестовом наборе данных всё выглядит довольно неплохо. Однако при попытке отрисовать реальные данные (линии метрополитена) возник ряд неприемлемых артефактов (вылеты линий за пределы экрана, исчезновение линий на определённых масштабных уровнях), в связи с чем была принята попытка поиска альтернативного способа нахождения параллельных кривых.

Стоит отметить, что во время написания данной статьи, в код Leaflet.PolylineOffset был добавлен коммит #e2166fa, устраняющий большинство из вышеописанных артефактов. Однако проблемы с отображением сегментов на мелком масштабе остались.

Артефакты при использовании плагина Leaflet.PolylineOffset

Если посмотреть код Leaflet.PolylineOffset, то становится понятно, что это легковесный плагин, реализующий в том числе и всю математику по расчету параллельных кривых. Однако нахождение параллельных кривых — это отнюдь не тривиальная задача, более того, подобной функции нет даже в JTS Topology Suite. Вот что говорит об этом один из основных разработчиков JTS Topology Suite Martin Davis:

In fact my original goal was to develop an offset line algorithm, but it turned out to be quite tricky to implement. I’m still thinking about doing offset lines, though.

Поэтому есть все основания не доверять тому алгоритму, который используется в Leaflet.PolylineOffset.

К сведению: реализация функции нахождения параллельных кривых имеется в библиотеке GEOS, код.

Одна из наиболее известных и функциональных библиотек на JavaScript, предназначенных для выполнения всевозможных пространственных операций над объектами в двумерном пространстве — JSTS Topology Suite. Это JavaScript порт упомянутой выше библиотеки JTS Topology Suite. Однако, как уже отмечалось, в JTS Topology Suite нет функции построения параллельных кривых, поэтому нет его и в JSTS Topology Suite. Можно было бы, конечно, разобраться в алгоритме, реализованном в GEOS и перенести его на JavaScript, используя соответствующие функции JSTS Topology Suite, но мы рассмотрим другой вариант, не столь точный, но как показала практика — вполне достаточный для решения конкретной задачи: визуализировать различные маршруты, физически проходящие по одному месту, без ощутимых артефактов. Не факт, что описанный ниже алгоритм будет приемлемо работать с другим набором данных, но все равно — будет хотя бы какая-то отправная точка.

В JSTS Topology Suite есть возможность построения одностороннего буфера (в ту или иную сторону в зависимости от знака). Пример построения одностороннего буфера (синяя линяя — внешнее кольцо построенного полигона, зелёная — исходная линия):

Односторонний буфер

Также в JSTS Topology Suite есть возможность построения «сырой» параллельной кривой (допускающей самопересечения). Пример построения такой кривой (черная линия — «сырая» кривая, красные точки — её узлы):

«Сырая» параллельная кривая

Итоговую параллельную кривую (голубая) будем набирать из узлов «сырой» кривой, касающихся внешнего кольца одностороннего буфера:

Итоговая параллельная кривая

Код получившейся функции расчета параллельной кривой:

Код всего модуля модуля можно взять на гитхабе. Чтобы склонировать его себе, выполните команду:

Там же есть и примеры использования.

В итоге мы получили результат, который на определенном масштабном уровне также содержит небольшие артефакты, но уже не в том количестве, как Leaflet.PolylineOffset. Никаких вылетов и исчезновений линий не наблюдается.

Результат

Источник

Как построить кривую, параллельную исходной кривой

Конструктор по сути (машиностроитель)

параллель получится только к прямой (отрезку)

Кривую линию можно только скопировать. Офсет изменит форму, уменьшит/увеличит радиус

Конструктор по сути (машиностроитель)

Boxa, в определении параллельности, кроме непересечения есть ещё и постоянство расстояния. Офсет кривых этого не дает:

А как мерить расстояние между кривыми? Если перпендикулярно касательной в точке, то оффсет дает равные расстояния. А если перпендикулярно некой оси(на рисунке выше перпендикулярно горизонтали), то надо кривую просто скопировать на нужное расстояние. При этом «не пересекаться» кривые не смогут.

Сейчас посмотрел определение параллельности кривых в википедии. Оффсет дает именно параллельность. Правда с ограничениями.

Конструктор по сути (машиностроитель)

Тоже так думал, но оказалось что нет.

Параллельная кривая или эквидистанта плоской кривой — огибающая семейства окружностей равного радиуса, центры которых лежат на заданной кривой. Понятие параллельной кривой — обобщение понятия параллельной прямой на случай плоских кривых. [Википедия]

Конструктор по сути (машиностроитель)

Bull, по Вашей логике, вот такие прямые (частный случай кривой) так же не параллельны: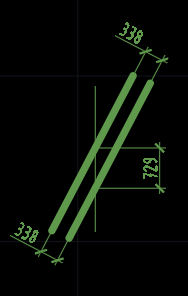

Вы серьезно считаете это правильным?

Первое что попалось под руку. Книга «Освоение Autodesk AutoCAD 2004» стр.279:
«Создание параллельных линий, параллельных кривых и концентрических окружностей. Команда OFFSET позволяет создавать параллельные линии, параллельные кривые и концентрические окружности, беря за основу уже существующие объекты. «

P.S.1 Да и в справке тоже: ПОДОБИЕ (команда) Создание концентрических окружностей, параллельных отрезков и кривых.

Конструктор по сути (машиностроитель)

Источник

параллельные кривые

Смотреть что такое «параллельные кривые» в других словарях:

Кривые второго порядка — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия

ЛЯПУНОВА ПОВЕРХНОСТИ И КРИВЫЕ — класс поверхностей и кривых, обладающих достаточно хорошими свойствами гладкости, введенный в теории потенциала А. М. Ляпуновым в кон. 19 нач. 20 вв. Поверхность Sв трехмерном евклидовом пространстве R3 наз. поверхностью Ляпунова, если выполнены… … Математическая энциклопедия

Кривая Безье — Кривые Безье или Кривые Бернштейна Безье были разработаны в 60 х годах XX века независимо друг от друга Пьером Безье (Pierre Bézier) из автомобилестроительной компании «Рено» и Полем де Кастельжо (Paul de Faget de Casteljau) из компании «Ситроен» … Википедия

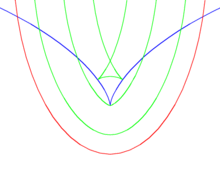
Параллельная кривая — Эллипс (показано красным), его эволюта (синий) и несколько параллельных кривых (зеленый). Обратите внимание как изламываются параллельные кривые, касающиеся эволюты … Википедия

НЕЕВКЛИДОВА ГЕОМЕТРИЯ — геометрия, сходная с геометрией Евклида в том, что в ней определено движение фигур, но отличающаяся от евклидовой геометрии тем, что один из пяти ее постулатов (второй или пятый) заменен его отрицанием. Отрицание одного из евклидовых постулатов… … Энциклопедия Кольера

Кривая второго порядка — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида в котором по крайней мере один из коэффициентов отличен от нуля. Содержание 1 История 2 … Википедия

Кривая 2-го порядка — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия

Фокальная ось — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия

Фокальная хорда — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия

Фокальный параметр — Кривая второго порядка геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида a11x2 + a22y2 + 2a12xy + 2a13x + 2a23y + a33 = 0, в котором по крайней мере один из коэффициентов отличен от нуля.… … Википедия

ГЕОМЕТРИЯ — раздел математики, занимающийся изучением свойств различных фигур (точек, линий, углов, двумерных и трехмерных объектов), их размеров и взаимного расположения. Для удобства преподавания геометрию подразделяют на планиметрию и стереометрию. В… … Энциклопедия Кольера

Источник

Кривые линии в начертательой геометрия

Содержание:

Любую кривую линию можно рассматривать с помощью двух подходов:

а) геометрический подход – линия является упорядоченной совокупностью точек (рис. 3.1 а);

б) кинематический подход (от греческого κινεµα – движение) – линия является траекторией точки (рис. 3.1 б).

Способы задания кривых линий

Бесконечную совокупность кривых можно разделить на такие виды:

а) по математической форме записи:

1) алгебраические – кривые, которые задаются алгебраическими уравнениями в данной системе координат. Например,

2) неалгебраические – кривые, которые задаются системой параметрических уравнений (см. п. 3.1.1.2 –3.1.1.6, 3.1.2). Например: (t – переменный параметр);

б) по размещению в пространстве

1) плоские– кривые, все точки которых принадлежат плоскости;

2) пространственные – кривые, точки которых не принадлежат одной плоскости (см. п. 3.1.2).

Алгебраические кривые, в зависимости от степени уравнения, которым они описаны, подразделяются на кривые второго порядка и кривые высших порядков (см. п. 3.1.1.1.2). Алгебраические кривые удобно задавать геометрическим способом.

К плоским алгебраическим кривым второго порядка относятся линии, которые описываются таким алгебраическим уравнением:

Форма кривой зависит от соотношений коэффициентов a, b, c, d этого уравнения.

Конические сечения

Существуют три основных вида конических сечений: эллипс, гипербола, парабола. Кроме того, существуют их отдельные и вырожденные формы: окружность, как отдельный случай эллипса; две прямые, как крайний случай гиперболы; прямая, как крайний случай параболы; точка, как крайний случай окружности.

Плоские алгебраические кривые второго порядка

Аполлоний Пергский (‘Aπολλώνιος ό Περγαϊος) – математик Древней Греции, один из трёх (наряду с Эвклидом и Архимедом) великих геометров античности. В произведении «Конические сечения» ввёл понятия «эллипс», «гипербола», «парабола». Один из исследователей неравномерного движения планет.

Гипербола (от греческого ύπερβολή – избыток) – геометрическое место точек М плоскости, разность расстояний от которых до двух заданных фокусов F1, F2 постоянно (рис. 3.3 б). Гипербола имеет две взаимно перпендикулярные оси симметрии х, у, которые пересекаются в точке, равноудаленной от его фокусов F1, F2. Гипербола имеет две ветви, сбоку каждой из которых есть фокус. Гипербола является контуром сечения конуса плоскостью параллельной его оси.

Парабола (от греческого παραβολή – дополнение) – геометрическое место точек М, равноудаленных от его фокуса F и прямой d – директрисы (рис. 3.3 в). Парабола имеет одну ось симметрии, которая проходит через фокус F перпендикулярно директрисе d. Парабола является контуром сечения конуса плоскостью, параллельной его образующей линии (см. п. 4.2.1, рис. 4.15).

С кинематической точки зрения плоские кривые второго порядка являются возможными траекториями космических тел. Например, по первому закону Кеплера все планеты Солнечной системы движутся по эллипсам, одним из фокусов которых является Солнце.

Плоские алгебраические кривые строят как лекальные кривые – линии, построенные с помощью специального чертёжного инструмента – лекала.

Для построения эллипса строятся две концентрические окружности с радиусами, которые равны полуосям a, b эллипса. Деление окружностей на равное количество N частей (как правило, N = 12) позволяет определить вспомогательные точки Искомые точки 1, 2, …, N эллипса являются точками пересечения вспомогательных горизонтальных и вертикальных линий, проведенных из соответствующих вспомогательных точек (рис. 3.4 а).

Построение эллипса (а) и гиперболы (б)

Иоганн Кеплер (Johannes Kepler) – немецкий математик, астроном, оптик. Один из основоположников современной астрономии. Открыл законы движения планет, базируясь на многочисленных наблюдениях датского ученого астронома Тихо Браге.

Для построения гиперболы выбираются две точки О, А (рис. 3.4 б). Из точки А проводятся два взаимно перпендикулярных луча l, m под углом 45° к горизонту. Из точки О строятся лучи k1, k2, … и определяются точки их пересечения с лучами l, m. Из полученных точек проводятся линии, параллельные l, m, до пересечения. Точки пересечения 1, 2, … принадлежать гиперболе. Они симметрично отображаются относительно горизонтальной оси. Искомая гипербола проходит через точки …, 2, 1, А, 1, 2, …

Для построения параболы (рис. 3.5) посередине между заданным фокусом F и директрисой d строится точка О пересечения параболы. Строится множество концентрических окружностей (с центром в фокусе F, радиусами …) и множество параллельных директрисе d прямых, удаленных от неё на расстояния … Точки 1, 2, … параболы являются точками пересечения построенных параллельных прямых с соответствующими концентрическими окружностями. Парабола строится по точкам …, 2, 1, О, 1, 2, …

Существуют и другие способы построения эллипса, гиперболы и параболы. Способами компьютерной техники плоские кривые строятся с помощью процедур интерполяции, в том числе с помощью кривой Бернштейна-Безье, числовых интерполяций и т.д.

Построение параболы

Кривые высших порядков

К плоским алгебраическим кривым высших порядков принадлежат линии, которые описываются алгебраическими уравнениями третьего и высшего порядков. Существует бесконечное количество таких кривых. Однако, для их изучения достаточно рассмотреть только основные виды.

Кубическая парабола – плоская кривая третьего порядка, которая описывается уравнением (рис. 3.6 а).

Парабола Нейла – плоская кривая третьего порядка, которая описывается уравнением (рис. 3.6 б). Она является траекторией точки, которая за равные промежутки времени опускается на одинаковые вертикальные отрезки. Эту кривую исследовал Вильям Нейл (1637 – 1670) – английский математик, астроном, член Королевского общества. Он решил задачу по определению длины дуги этой кривой.

Кубическая парабола (а) и парабола Нейла (б)

Лист Декарта – плоская кривая третьего порядка, для которой сумма объёмов кубов, построенных на координатах х, у, равна объёму прямоугольного параллелепипеда со сторонами х, у, а (рис. 3.7) . Эта кривая названа в честь Рене Декарта, который отправил письмо Пьеру Ферма со сформулированной задачей на объёмы обозначенных тел.

Локон Аньези – плоская кривая третьего порядка, которая строится таким способом (рис. 3.8). Строится окружность диаметром ОС. Из точки О проводятся отрезки , …, концы которых находятся на линии а, перпендикулярной диаметру ОС. Находятся точки В1, В2, … пересечения отрезков … с окружностью. Точки 1, 2, … кривой являются точками пересечения горизонтальных и вертикальных линий, проведенных из точек А1, А2, …, В1, В2, …

Лист Декарта Локон Аньези

Циссоида Диокла (от греческого χισσος – плющ) – плоская кривая третьего порядка, которая строится таким способом (рис. 3.9). Из точки О окружности диаметром ОС проводятся отрезки ОА1, ОА2, …, концы которых находятся на линии а, перпендикулярной ОС. Находятся точки В1, В2, … пересечения этих отрезков с окружностью. Из точек А1, А2, … откладываются отрезки …, длины которых равны длинам отрезков ОВ1, ОВ2, … По точкам …, 2, 1, О, 1, 2, … строится искомая линия.

Впервые циссоида была исследована Диоклом (246 до н. э –180 до н. э.) – математиком Древней Греции часов Аполлония Пергского. В его произведении «О зажигательных зеркалах» с помощью этой кривой решены задачи по удвоению объёма куба и по построению пропорциональных отрезков.

Циссоида Диокла

Строфоида (от греческого στροφή – оборот) – плоская кривая третьего порядка, которая строится таким способом (рис. 3.10). Из точки С оси у проводятся лучи СА1, СА2, … Точки А1, А2, … принадлежат оси х. На построенных лучах по обе стороны от точек А1, А2, …откладываются отрезки … и , … с длинами, равными длинам , … Искомая линия проходит через точки

Исследованиями строфоиды занимался Ж. Роберваль в 1645 г. Первым названием строфоиды была птероида (от греческого πτερος – крыло). Линия получила нынешнее название в 1849 г.

Строфоида

Рене Декарт (René Descartes) – французский философ, физик, математик, физиолог. Создал аналитическую геометрию и ввёл современную алгебраическую символику. Автор философского метода радикального сомнения. Основатель механицизма в физике. Основал рефлексологию.

Мария Гаэтана Аньези (Maria Gaetana Agnesi) – итальянский математик, профессор Болонского университета. Автор трудов по дифференциальному исчислению и аналитической геометрии. Автор работы «Основы анализа для итальянского юношества ».

Овал Кассини – геометрическое место точек М плоскости, произведение а расстояний от которых до двух заданных фокусов F1, F2 является постоянным (рис. 3.11).

Для лемнискаты Бернулли произведение а в четыре раза меньше квадрата расстояния F1F2 между фокусами.

Овалы Кассини

Жиль Роберваль (Персонье) (Gilles Personne de Roberval) – выдающийся французский математик, физик, астроном, член Парижской академии наук. Занимался проблемами бесконечно малых величин. Изобрёл оригинальные способы определения объёмов тел. Автор кинематического способа построения касательной к кривой линии. Внёс значительный вклад в теорию тригонометрических функций.

Джованни Доменико Кассини (Giovanni Domenico Cassini) – итальянский и французский астроном, инженер. Автор теории атмосферной рефракции. Открыл четыре спутника Сатурна, Автор большой карты Луны. Определил расстояние от Земли до Марса. Ошибочно считал, что орбитами планет являются построенные им овалы.

Кривая Персея – плоская кривая четвертого порядка, которая является линией пересечения открытого тора (см. п. 4.2.1, табл. 4.1, рис. 4.13) плоскостью Σ, параллельной его оси (рис. 3.12). Эта линия названа в честь древнегреческого геометра Персея (ІІ ст. до н. э.), который провёл исследования разных способов задания кривых линий.

Плоские алгебраические кривые четвёртого порядка

Частным случаем кривой Персея является лемниската Бута, названная в честь английского математика Джеймса Бута. Эта линия образуется, когда секущая плоскость Σ является касательной к внутренней образующей линии тора (см. п. 4.2.1, рис. 4.16).

Конхоида Никомеда (от греческого κωνχος – раковина, εϊδος – вид) – линия, которая образуется изменением (увеличением или уменьшением ) на постоянную величину а расстояний от начала отсчёта О до каждой точки М прямой l (рис. 3.13).

Конхоида Никомеда Улитка Паскаля

Конхоида Никомеда является плоской кривой четвертого порядка и названа в честь древнегреческого математика, который жил в ІІІ ст. до н. э. и занимался проблемой квадратуры окружности и трисекции угла.

Якоб Бернулли (Jacob Bernoulli) – швейцарский математик, профессор Базельского университета. Внёс значительный вклад в развитие аналитической геометрии и зарождения вариационного исчисления. Значительных достижений добился в теории чисел и рядов, теории вероятностей. Автор термина «интеграл». Заложил основы изучения лемнискат.

Улитка Паскаля – линия, которая образуется изменением (увеличением или уменьшением) на постоянную величину а расстояние от начала отсчёта О до каждой точки М окружности.

Эта линия посвящена Этьену Паскалю (1623 – 1662) – королевскому чиновнику, отцу выдающегося ученого Блэза Паскаля.

На рис. 3.14 построена улитка Паскаля для случая, когда начало отсчёта О удалено от окружности на величину радиуса. Значение а равно радиусу окружности.

Овал Декарта – геометрическое место точек плоскости, расстояния MF1, MF2 от каждой точки М которой до двух фокусов F1, F2 связаны линейным соотношением = с (рис. 3.15), где a, b, c –постоянные параметры.

Овал Декарта не является овалом по определению (см. п. 3.1.1.7, рис. 3.38 а), а является кривой четвертого порядка. При определённых значениях а, b, с он вырождается в эллипс или окружность, гиперболу, параболу, улитку Паскаля.

Тригонометрические кривые

К тригонометрическим кривым относятся плоские кривые линии, которые описываются тригонометрическими уравнениями у = sinx, y = cosx, y = tgx, y = ctgx, или уравнениями на их основе. Поскольку все тригонометрические функции можно выразить через функцию, например, синуса, рассмотрим только синусоиду.

Синусоида – траектория точки М, которая равномерно движется по окружности радиусом а, которое скользит без качения по плоской поверхности.

Для построения синусоиды (рис. 3.16) строится окружность радиусом а. Последняя делится на равное количество N частей (как правило, N = 12). Из крайней правой точки 1 окружности строится горизонтальный отрезок длина которого равна длине окружности 2πа. Отрезок делится на N равных частей. Из точек 1, 2, …, N окружности и отрезка проводятся вертикальные и горизонтальные линии до их взаимного пересечения. Точки 1, 2, … пересечения этих линий является точками искомой синусоиды.

Синусоида

Первые исследования синусоиды начались в Древней Индии. Сначала эта кривая называлась «арха-джива», что означает «полу тетива». Позже слово трансформировалось в «джайб» – «впадина». Европейский термин «sinus» был основан австрийским математиком Георгом фон Пойербахом (1423 – 1461), который составил таблицу значений этой функции. Значительный вклад в развитие тригонометрических функций внёс выдающийся французский математик Ж. Роберваль. Он впервые в 1634 г. построил синусоиду.

Циклоидальные кривые

К классу циклоидальных кривых принадлежат траектории точки окружности, которая движется по неподвижной поверхности без скольжения.

Циклоида (от греческого κυκλοειδής – круглый) – траектория точки окружности, которая катится по прямой без скольжения.

Для построения циклоиды (рис. 3.17) окружность заданного радиуса а делится на N равных частей (например, N = 12). Эта окружность равномерно дублируется N раз (с шагом 2πа/N) в направлении луча, который выходит из центра О окружности. Из точек … окружности проводятся горизонтальные лучи до пересечения с построенными окружностями. В результате по полученным точкам 1, 2, … строится циклоида.

Циклоида

Первым названием циклоиды была «рулета». Термин «циклоида» ввёл Галилео Галилей, современники которого изучали эту кривую. Доказательные исследования циклоиды принадлежат Я. Бернулли.

Перевернутая циклоида называется брахистохроной – кривой скорейшего спуска материальной точки.

Х. Гюйгенс открыл свойство точки сохранять период собственных колебаний во время движения по перевернутой циклоиде. Это свойство было использовано им при создании точных часов.

Галилео Галилей (Galileo Galilei) – итальянский физик, механик, астроном, философ, математик, который сделал значительный вклад в науку своего времени. Он впервые использовал телескоп для исследования небесных тел и совершил многочисленные астрономические открытия. Галилей является основателем экспериментальной физики. Своими экспериментами он «уничтожил» метафизику Аристотеля и заложил фундамент классической механики.

Христиан Гюйгенс (Chrisiaan Huygens) – нидерландский физик, механик, математик, астроном, изобретатель, президент Парижской академии наук. Изобрёл маятниковый механизм, а также точные карманные часы. Открыл кольца Сатурна и один из его спутников. Открыл теорию эвольвент и эволют. Заложил основы теории вероятностей. Его «Книга мирозрения» является первой переведенной на Руси книгой, где изложена гелиоцентрическая теория Коперника.

Эпициклоида (от греческого έπί – над, κυκλος – окружность) – траектория точки окружности радиусом r, которая катится по внешней стороне окружности радиусом R без скольжения. Существует бесконечное количество эпициклоид, форма которых зависит от соотношения а = R/r радиусов окружностей. При а = 1 эпициклоида называется кардиоидой (от греческого καρδιοειδές – сердцеобразный). На рис. 3.18 а построена кардиоида. Окружность заданного радиуса катится по центральной окружности такого же радиуса. Качение условно моделируется двенадцатью положениями окружности. С помощью вспомогательных точек и дуг окружностей, которые выходят из этих точек, находятся точки 1, 2, …, 12 пересечения дуг с совокупностью построенных окружностей. По точкам 1, 2, …, 12 строится кардиоида.

Эпициклоиды

Первые упоминания про кардиоиду встречаются в труде французского ученого Луи Карре (1705 р.). Название этой линии в 1741 г. дал итальянский ученый Джованни Кастиллоне. Кардиоида, кроме того, что принадлежит классу циклоидальных кривых, также является отдельным случаем улитки Паскаля (см. п. 3.1.1.1.2, рис. 3.14).

В случае, когда а = 2, эпициклоида называется нефроидой (от греческого νεφρόειδής – почкообразный). На рис. 3.18 б построена нефроида. Окружность заданного радиуса катиться по центральной окружности вдвое большего радиуса. Качение условно моделируется двенадцатью положениями меньшей окружности. С помощью вспомогательных точек и дуг окружностей, которые выходят из этих точек, находятся точки 1, 2, …, 12 пересечения дуг с совокупностью построенных окружностей. По точкам 1, 2, …, 12 строится нефроида.

Гипоциклоида (от греческого γιπό – под, κυκλος – окружность) – траектория точки окружности радиусом r, которая катится по внутренней стороне окружности радиусом R без скольжения.

Среди бесконечного числа гипоциклоид, форма которых зависит от соотношения радиусов окружностей а = R/r, необходимо выделить такие. При а = 3 гипоциклоида называется кривой Штейнера, или дельтоидой (от греческого δελτοειδής – дельтообразный). На рис. 3.19 а построена дельтоида. Окружность заданного радиуса катится по внутренней стороне окружности втрое большего радиуса. Качение условно моделируется восемнадцатью положениями меньшей окружности. С помощью точек и дуг окружностей, которые выходят из этих точек, находятся точки 1, 2, …, 18 пересечения дуг с совокупностью построенных окружностей. По точкам 1, 2, …, 18 строится кривая Штейнера (дельтоида).

Гипоциклоиды

В случае, когда а = 4, гипоциклоида называется астроидой (от греческого αστέριειδής – звёздообразный). На рис. 3.19 б построена астроида. Окружность заданного радиуса катится по внутренней стороне окружности вчетверо большего радиуса. Качение условно моделируется двадцатью четырьмя положениями меньшей окружности. С помощью вспомогательных точек и дуг окружностей, которые выходят из этих точек, находятся точки 1, 2, …, 24 пересечения дуг с совокупностью построенных окружностей. По точкам 1, 2, …, 24 строится астроида.

Линии класса циклоид являются одними из наиболее распространённых кривых в машиностроении, поскольку являются траекториями точек деталей механизмов и машин. Например, точки автомобильных колёс движутся по циклоидальным и трохоидальным траекториям; точки сцепления зубчатых колёс планетарных и дифференциальных передач движутся по эпи- и гипоциклическим траекториям.

Трохоида (от греческого τροχοειδής – колесообразный) – траектория непериферической точки окружности, которая катится по прямой без скольжения.

Для построения трохоиды (рис. 3.20) окружность заданного радиуса r делится на N равных частей (например, N = 12). Эта окружность вместе с окружностью радиусом R равномерно (с шагом 2πа/N) дублируется N раз в направлении луча, который выходит из центра О. Из точек … окружности радиусом r проводятся лучи до пересечения с построенными окружностями. В результате по полученным точкам 1, 2, … строится трохоида

На практике трохоида используется в электровакуумных приборах для перемещения электронов. Трохоидальное сцепление используется в шестеренных гидромашинах.

Якоб Штейнер (Jacob Steiner) – швейцарский математик, член Берлинской академии наук. Основатель синтетической геометрии кривых линий и поверхностей.

Трохоида

Эпитрохоида (от греческого έπί – над, τροχος – колесо) – траектория непериферической точки круга радиусом r, который катится по внешней стороне окружности радиусом R без скольжения.

На рис. 3.21 а показан простейший вид эпитрохоиды. Для её построения круг заданного радиуса катится по центральной окружности того же радиуса. Качение условно моделируется восемью положениями круга. Кругу принадлежит точка, которая находится на половине радиуса от его центра. С помощью вспомогательных точек …, 8 и дуг окружностей, которые выходят из этих точек, находятся точки 1, 2, …, 8 пересечения дуг с совокупностью построенных окружностей. По точкам 1, 2, …, 8 строится эпитрохоида.

Эпи- и гипотрохоида

Построенная на рис. 3.21 а эпитрохоида является улиткой Паскаля (см. п. 3.1.1.1.2, рис. 3.14). Гипотрохоида – (от греческого γιπό – под, τροχος – колесо) – траектория непериферической точки круга радиусом r, который катится по внутренней стороне окружности радиусом R без проскальзывания.

На рис. 3.21 б показан простейший вид гипотрохоиды. Для её построения круг заданного радиуса катится по внутренней поверхности окружности вдвое большего радиуса. Качение условно моделируется восемью положениями круга. Кругу принадлежит точка, которая находится на половине радиуса от его центра. С помощью вспомогательных точек , …, и дуг окружностей, выходящих из этих точек, находятся точки 1, 2, …, 8 пересечения дуг с совокупностью построенных окружностей. По точкам 1, 2, …, 8 строится гипотрохоида.

Построенная на рис. 3.21 б гипотрохоида является эллипсом (см. п. 3.1.1.1.1, рис. 3.4 а).

Спиральные кривые

Любая спиральная кривая (от латинского spira – изгиб) является траекторией точки, движущейся по прямой, которая вращается вокруг неподвижного центра. Среди большого количества спиральных кривых необходимо выделить такие.

Спираль Архимеда – траектория точки, равномерно движущейся по прямой, равномерно вращающейся вокруг неподвижной точки.

Для построения спирали Архимеда (рис. 3.22) окружность заданного диаметра делится на N равных частей … (как правило, N = 12). Из центра О окружности строятся N отрезков О-1, О-2, …, один из которых О-12 делится на N равных частей точками , … С помощью дуг окружностей находятся точки 1, 2, … Спираль Архимеда строится по точкам О, 1, 2, …

Спираль Архимеда

Архимед из Сиракуз (Άρχιµήδης) – древнегреческий математик, физик, механик и инженер-изобретатель. Совершил множество открытий в геометрии. Заложил основы механики и гидростатики.

Изогональная спираль (от греческого ίσος – равный, γωνία – угол) – траектория точки М, неравномерно движущейся по прямой линии l, которая равномерно вращается вокруг неподвижной точки О, причём угол χ между касательной (см. п. 3.3) и радиусом-вектором r (вектором, начало которого совпадает с началом отсчёта О, конец – с данной точкой М) не изменяется (рис. 3.23).

Логарифмическая спираль

Изогональная спираль является логарифмической, поскольку угол φ между радиусом-вектором r точки М и горизонтальной осью х пропорционален натуральному логарифму от модуля r: φ = ln(r). Исследованиями логарифмической спирали занимался швейцарский математик Я. Бернулли.

Логарифмическая кривая является линией, которой могут быть описаны строение Вселенной, природные явления, живые существа и т.д. Например, на рис. 3.24 а показана галактика Водоворот; на рис. 3.24 б – зона низкого давления над Исландией; на рис. 3.24 в – раковина моллюска.

Проявления логарифмических спиралей

Клотоида (от греческого κλωθοειδής – ниткообразный) – линия, радиус кривизны которой (см. п. 3.4.2) пропорционален длине дуги (рис. 3.25).

Спираль Корню

Другое название клотоиды – спираль Корню – посвящено французскому физику, который использовал эту кривую в исследованиях дифракции света.

Клотоида используется как переходная дуга в дорожном строительстве. Форма дороги в форме клотоиды позволяет преодолевать повороты без существенного снижения скорости и с равномерным вращением руля.

Для приблизительного построения клотоиды (рис. 3.26) из точек О, 1 проводятся две окружности заданного радиуса . Проводится окружность радиусом 2а, касательная к отрезку О1 (в точке 1) с центром в точке Из точки 1 строится окружность радиусом а до пересечения с окружностью радиусом 2а. Проводится окружность радиусом 3а, касательная к отрезку 1 – 2 (в точке 2) с центром в точке . Из точки 2 строится окружность радиусом а пересечения с окружностью радиусом 3а … Приближённой клотоидой является линия, проходящая через точки 1, 2, …

Построение клотоиды

Спираль Ферма – траектория точки М, неравномерно движущейся по прямой l, вращающейся вокруг неподвижного центра O, причём угол φ между радиусом-вектором r и горизонтальной осью пропорционален квадрату длины r: φ = (рис. 3.27 а).

Спираль Ферма (а) и параболическая спираль (б)

Пьер де Ферма (Pierre de Fermat) – французский математик, юрист, полиглот. Один из основателей аналитической геометрии, математического анализа, теории вероятностей и теории чисел. Автор Большой теоремы Ферма. Советник Тулузского парламента.

Параболическая спираль часто встречается в природе (рис. 3.28 а) и технике (рис. 3.28 б), например, определяет профиль твердосплавных свёрл по бетону, кирпичу и керамике.

– Проявления и применение спиральных кривых

Кроме выше обозначенных, существует также большое количество других видов спиралей:

б) спираль Галилея: (рис. 3.29 б);

в) жезл: (рис. 3.29 в) и т.д..

Спиральные кривые

Трансцендентные кривые

Плоской трансцендентной кривой (от латинского transcendo – переступать) является линия, которую невозможно описать уравнением, которое прямо связывает координаты х, у каждой точки М. Как правило, трансцендентные кривые задаются системой параметрических уравнений(см. с. 21).

Среди большого разнообразия трансцендентных кривых выделяют такие.

Квадратриса Динострата (от латинского quadro – площадь) – траектория точки М пересечения двух прямых h, r, первая из которых равномерно опускается по вертикали, вторая – равномерно вращается вокруг неподвижной точки О (рис. 3.30 а).

Квадратриса Динострата

Для построения квадратрисы (рис. 3.30 б) четверть окружности а делится на N равных частей (например, N = 6) точками … Из центра О окружности проводятся отрезки , … Радиус делится на N равных частей точками , … Точки 1, 2, … пересечения отрезков … с горизонтальными лучами, проведенными из точек , …, являются точками квадратрисы.

Трактриса (от латинского trahere – волочить) – плоская кривая, любая точка М которой удалена от оси х в направлении касательной (см. п. 3.3) на одинаковое расстояние а (рис. 3.31 а).

Трактриса

Первые упоминания о квадратрисе принадлежат Паппу Александрийскому и Ямвлоху и датируются концом ІІІ ст. Кривая открыта софистом Гиппием из Элиды в V ст. до н. э. и использована им для решения задачи про трисекцию угла – деление угла на три равные части. Динострат в конце ІV ст. до н. э. с помощью квадратрисы решал задачу про квадратуру круга – построение квадрата, площадь которого равна площади данного круга.

Трактриса изобретена в 1670 г. К. Перро. Свойства трактрисы исследовали Исаак Ньютон, Христиан Гюйгенс, Готфрид Вильгельм фон Лейбниц.

П. Бугер решил задачу Леонардо да Винчи на определение формы верёвки, которой тащат предмет по горизонтальной поверхности, и установил, что эта линия является трактрисой.

Трактриса также является кривой погони – решением такой задачи. Пусть точка А движется равномерно прямолинейно. Необходимо найти линию, по которой должна двигаться точка М так, чтобы прямая АМ была к ней касательной (рис. 3.31 а).

Для приближённого построения трактрисы (рис. 3.31 б) на оси у откладывается отрезок заданной длины а. Вдоль оси х последовательно откладываются одинаковые отрезки …, длина которых значительно меньше величины а. Из точки строится окружность радиусом а и определяется точка 1 её пересечения с осью у. Из точки строится окружность радиусом а и определяется точка 2 её пересечения с отрезком Из точки строится окружность радиусом а и определяется точка 3 её пересечения с отрезком … Трактриса приближённо строится по точкам О, 1, 2, …

Цепная линия – линия, форму которой приобретает цепь с закреплёнными концами (рис. 3.32 а).

Применение и проявления цепной линии

Клод Перро (Claude Perrault) – французский инженер, механик, архитектор, врач и математик. Брат известного сказочника Шарля Перро. Один из первых членов Французской академии наук. Автор Парижской обсерватории, Триумфальной арки, колоннады восточной части Лувра.

Пьер Бугер (Pierre Bouguér) – французский физик и астроном, основатель фотометрии. Известны его труды по теории кораблестроения, геодезии.

Имя Бугера внесено в список семидесяти двух величайших учёных Франции.

Фигуры Лиссажу

Фигуры Лиссажу – траектории точки, которая одновременно осуществляет два гармоничных колебания с разными частотами во взаимно перпендикулярных направлениях (рис. 3.33).

Фигуры Лиссажу

Впервые эти кривые были изучены Ж. Лиссажу. Фигуры Лиссажу строятся на мониторе электронного осциллографа (от латинского oscillo – колебаться – и греческого γραφω – писать) – устройства для исследования часовых и амплитудных параметров электрических сигналов, которые подаются на его входы (рис. 3.34).

Проявления фигур Лиссажу

Жуль Антуан Лиссажу (Jules Antoine Lissajous) – французский математик, член-корреспондент Парижской академии наук. Его научный посвящён вибрационной акустике решеток.

Одним из простейших видов фигур Лиссажу является лемниската Жероно – траектория точки, которая одновременно осуществляет два гармоничных колебания во взаимно перпендикулярных направлениях с частотами, которые отличаются вдвое(рис. 3.35 а). Эта линия названа в честь Камиля-Кристофа Жероно (1799 – 1891) – французского математика, профессора Парижской политехнической школы. Его научная деятельность посвящена проблемам геометрии и Диофантова анализа. Он является автором учебников по аналитической геометрии и тригонометрии и сооснователем научного журнала “Nouvelles Annales de Mathématiques”.

Построение фигур Лиссажу

Сопряжения

Сопряжением называется плавный переход от одной линии l к другой m, выполненный с помощью дуги окружности (рис. 3.36).

Любое сопряжение характеризуется такими параметрами:

а) центр сопряжения– центр О окружности, с помощью дуги которого строится сопряжение;

б) точки сопряжения– точки А, В начала и конца дуги, которой выполняется сопряжение;

в) радиус сопряжения – радиус R дуги, которой выполняется сопряжение.

Сопряжение

Свойства элементов сопряжения:

а) центр О сопряжения равноудален от точек А, В сопряжения, причём расстояния ОА, ОВ равны радиусу R сопряжения;

б) прямые перпендикулярные отрезкам ОА, ОВ, являются касательными (см. п. 3.3) к линиям l, m, которые сопрягаются ;

в) прямые ОА, ОВ проходят через центры кривизны (см. п. 3.4.2) линий l, m соответственно.

Существуют десять классических типов сопряжений:

а) сопряжение двух окружностей (рис. 3.37 а – є);

б) сопряжение двух прямых линий (рис. 3.37 ж);

в) сопряжение окружности и прямой (рис. 3.37 з – к).

Виды сопряжений

Для построения сопряжения двух окружностей (рис. 3.37 а – є) необходимо из центров этих окружностей провести дуги окружностей радиусами до их пересечения. Полученная точка является центром сопряжения. Значения радиусов в зависимости от типа сопряжения приведены в табл. 3.1. Из центра О сопряжения строится дуга окружности радиусом R и находятся точки А, В сопряжения.

Для построения сопряжения двух прямых (рис. 3.37 ж) проводятся линии, им параллельные и расположенные на расстоянии R. Точкой пересечения прямых является центр сопряжения, из которого проводится дуга окружности радиусом R, и определяются точки А, В сопряжения.

Для построения сопряжения окружности и прямой (рис. 3.37 з – к) из центра окружности проводится окружность радиусом (табл. 3.1). Строится линия, параллельная заданной прямой, на расстоянии R. Из центра сопряжения, который является точкой пересечения построенных окружности и прямой, строится дуга окружности радиусом R и определяются точки А, В сопряжения.

К отдельному классу сопряжений относятся коробовые кривые – совокупности дуг окружностей (с кривизной одного направления),которые в точках перехода имеют общие касательные (рис. 3.38).

Коробовые кривые

К коробовым кривым относятся такие линии:

а) овал (от французского ovalе – яйцо) – замкнутая линия, полученная одинаковыми по радиусам сопряжениями двух одинаковых эксцентрических окружностей (рис. 3.38 а);

б) овоид (от латинского ovum – яйцо, греческого εϊδος – вид) – замкнутая линия, полученная одинаковыми по радиусам сопряжениями двух разных эксцентрических окружностей (рис. 3.38 б);

в) завиток – кривая, которая выполняется с помощью сопряжения двух окружностей разных диаметров, одна из которых полностью находится в середине другой (рис. 3.38 в).

Для построения овала (рис. 3.38 а) необходимо из центров двух окружностей провести дуги радиусами R – r до их пересечения. Полученные точки являются центрами сопряжений. Из центров строятся дуги окружностей радиусом R и находятся точки сопряжений.

Для построения овоида (рис. 3.38 б) необходимо из центров двух окружностей провести дуги радиусами до их пересечения. Полученные точки являются центрами сопряжений. Из центров строятся дуги окружностей радиусом R и находятся точки сопряжений.

Для построения завитка (рис. 3.38 в) необходимо из центров двух окружностей провести дуги радиусами до их пересечения. Полученная точка О является центром сопряжения. Из центра О строится дуга окружности радиусом R и находятся точки А, В сопряжения.

Коробовые кривые распространены в природе. Форму овала и овоида имеют магматические породы, известковые зерна, заготовительные изделия насекомых (рис. 3.39 а – б); в форме завитка встречаются соцветия растений, раковины улиток (рис. 3.39 в) и т.д..

Проявления коробовых кривых

Коробовыми кривыми условно можно заменить плоские кривые линии. Например,, эллипс упрощённо строится в форме овала (рис. 3.40 а), спираль Архимеда – в форме завитка (рис. 3.40 б) и т.д

.

Сравнение коробовых кривых с плоскими кривыми линиями

С развитием современных способов компьютерного моделирования сопряжение может быть выполнено не только с помощью дуги окружности, а и другой кривой, например, эллипсом (рис. 3.41).

Сопряжение произвольной плоской кривой

Винтовые линии

Винтовая линия– траектория конца М отрезка ОМ, который удлиняется или укорачивается и движется вдоль перпендикулярной ему оси і, равномерно вращаясь при этом вокруг этой оси (рис. 3.42).

Горизонтальная проекция винтовой линии (рис. 3.42 а) в общем случае является спиральной кривой, фронтальная – тригонометрической кривой.

Винтовые линии

Простейшими случаями винтовых линий являются цилиндрическая и коническая винтовые линии.

Цилиндрическая винтовая линия – траектория конца М отрезка ОМ, который равномерно движется вдоль его перпендикулярной оси і, равномерно вращаясь при этом вокруг этой оси (рис. 3.42 б).

Горизонтальная проекция цилиндрической винтовой линии является окружностью, фронтальная – синусоидой.

Коническая винтовая линия – траектория конца М отрезка ОМ, который равномерно удлиняется или укорачивается и равномерно движется вдоль перпендикулярной ему оси і, равномерно вращаясь при этом вокруг этой оси (рис. 3.42 в).

Горизонтальная проекция конической винтовой линии — это спираль Архимеда, фронтальная – тригонометрическая кривая.

Винтовые линии распространены в природе. Например, форму винтовых линий имеют молекула ДНК (рис. 3.43 а), ус растения (рис. 3.43 б).

Проявления и применение винтовых линий

Винтовые линии нашли своё применение в технике. В форме винтовых линий изготовляют сверлильный инструмент (рис. 3.43 в), пружины (рис. 3.43 г), шнеки мясорубок (рис. 3.43 д). Винт Архимеда, изобретённый ок. 250 р. до н. э., используется и сейчас как рабочий орган машины для осушения затопленных низин сельскохозяйственных угодий (рис. 3.43 е). Винтовые линии можно также строить по их развёрткам (см. п. 5.3). Например, цилиндрическая винтовая линия имеет развёртку в форме прямой линии (рис. 3.44).

Построение равномерной винтовой линии по развёртке

На рис. 3.45 по заданной горизонтальной проекции неравномерной цилиндрической винтовой линии и её развёртке в форме произвольной кривой построена фронтальная проекция винтовой линии.

Построение неравномерной винтовой линии по её развёртке

Примеры и образцы решения задач:

Услуги по выполнению чертежей:

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Источник