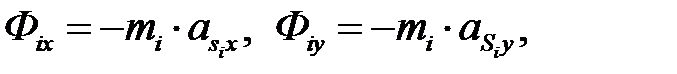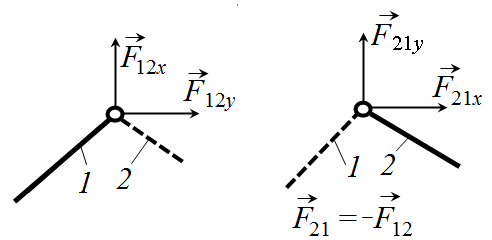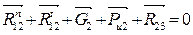Что является неизвестным при определении реакции во вращательной паре
Реакции в кинематических парах
Лекция 7
Силовой анализ механизмов аналитическим методом
Силовой расчет заключается в определении сил, действующих на звенья механизма, при известном законе движения начального звена. Силовой расчет является первой (прямой) задачей динамики.
Задачи силового расчета
1. Определение сил приложенных к звеньям механизма. Эти силы необходимы для расчета звеньев на прочность и жесткость.
2. Определение сил реакций в кинематических парах (КП). Значения полученных реакций используют для выбора типов и размеров подшипников из условия долговечности, вычисления коэффициента полезного действия механизма.
3. Определение уравновешивающего (или движущего) момента 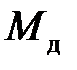
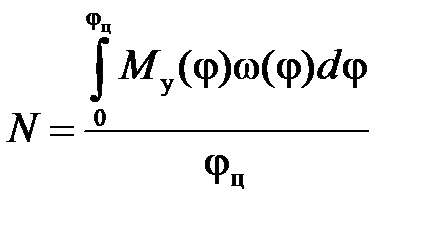
где 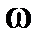
Допущения, принимаемые при силовом расчете плоских рычажных механизмов
1. Силы трения не учитываются.
2. Звенья считаются абсолютно твердыми телами.
3. Все силы действуют в одной плоскости.
4. Все звенья имеют плоскость симметрии, совпадающую с плоскостью движения.
Метод расчета
Для силового расчета обычно применяют принцип Д’Аламбера. Силовой расчет с применением этого принципа называюткинетостатическим.
Если в любой момент времени к каждой точке системы кроме действующих на нее внешних и внутренних сил присоединить силы инерции, то полученная система сил будет уравновешенной и к ней можно применить уравнения равновесия.
Звено является абсолютно твердым телом, к каждой точке которого приложена элементарная сила инерции. Элементарные силы инерции всех точек звена приводят к центру масс и заменяют главным вектором 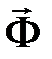
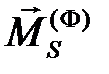
При плоскопараллельном движении звена главный вектор и главный момент сил инерции определяют по следующим формулам:
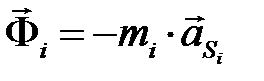
где 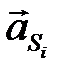
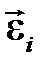
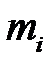
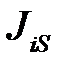
При поступательном движении звена 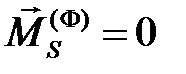
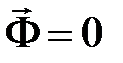
При аналитическом расчете плоских механизмов главный вектор сил инерции раскладывают по осям координат
а главный момент сил инерции определяют по формуле
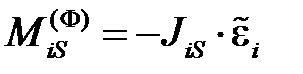
где 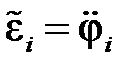
Обычно применяют следующее правило знаков: если 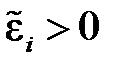
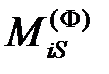
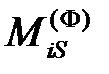
Уравнения равновесия звена с учетом сил инерции, называемыеуравнениями кинетостатики, имею вид

где 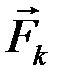
При аналитическом выполнении расчетов с использованием ЭВМ моменты сил удобно вычислять относительно начала координат (т.O) по формуле:
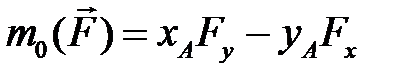
где 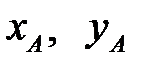

Реакции в кинематических парах
Силы взаимодействия звеньев (реакции в КП) обозначаютс двойным нижним индексом 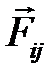
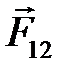
Рассмотрим реакции в кинематических парах, пренебрегая силами трения.
Сила реакцииво вращательной КП лежит в плоскости относительного движения звеньев. Модуль и направление реакции зависит от сил, действующих на звено, и определяются в результате силового расчета. При выполнении силового расчета аналитическим методом реакции во вращательных КП раскладывают на две составляющие по осям координат(рис. 7.1).
Рис.7.1. Реакция во вращательной КП
На расчетных схемах показывают положительные направления сил. По 3 закону Ньютона 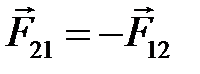
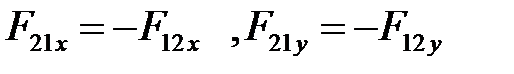
Во вращательной кинематической паре необходимо определять две неизвестные величины 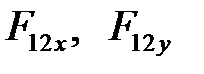
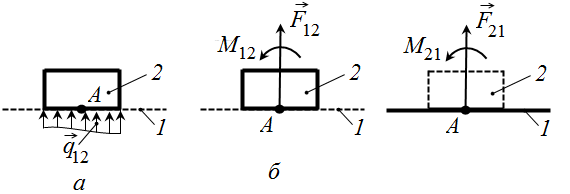
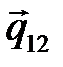
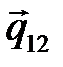
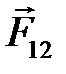
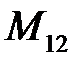
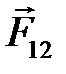
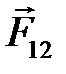
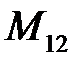
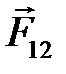
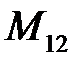
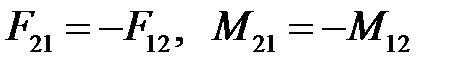
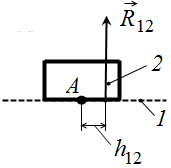
Рис. 7.2. Реакция в поступательной КП:
а – распределенная сила реакции 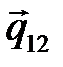
Если главный вектор 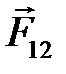
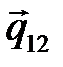
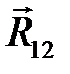
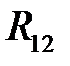
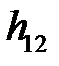
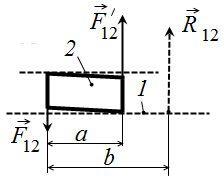
Рис.7.3. Равнодействующая распределенной реакции в поступательной КП
Следовательно, в поступательной паре КП необходимо определять две неизвестные величины 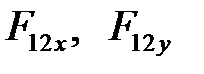
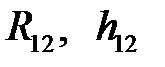
Примечание. Если точка приложения равнодействующей расположена вне поверхности соприкосновения звеньев, то на звено действуют две сосредоточенные силы, приложенные на границах поверхности соприкосновения (рис. 7.4). При этом
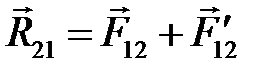
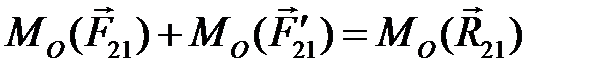
Высшая кинематическая пара.
В высшей кинематической пареконтакт звеньев может происходить по линии или в точке. При точечном контакте сила реакции является сосредоточенной, при линейном контакте – распределенной по линии.
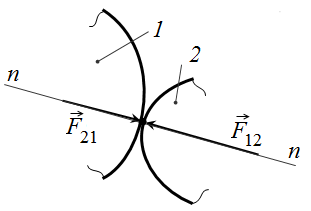
В высшей КП реакция направлена вдоль общей нормали (n-n), проведенной в точке касания (т. A)к двум соприкасающимся поверхностям 1 и 2 (рис. 7.5).
Рис. 7.5 Реакция в высшей кинематической паре
В высшей кинематической паре на плоскости необходимо определять одну неизвестную величину – модуль реакции.
Определение реакций в кинематических парах



3.1.4.1 Условие статической определимости кинематической цепи
При силовом расчете механизма закон движения ведущего звена является заданным. Также предполагаются известными массы и моменты инерции звеньев. Прежде всего, силовой расчет начинается с определения реакций.
Рассмотрим направление реакций в различных кинематических парах.
1. Реакция в поступательной кинематической паре V класса направлена перпендикулярно движению. Она известна по направлению, но неизвестны ее величина и точка приложения (рисунок 3.4, б).
2. Реакция во вращательной кинематической паре V класса проходит через центр шарнира, т.е. известна точка ее приложения. Величина и направление этой реакции неизвестны. Результирующая реакция R12 раскладывается на две составляющие: нормальная составляющая R n 12 направлена вдоль звена, а тангенциальная R t 12 – перпендикулярно звену (рисунок 3.4, а).
3. Реакция в высшей кинематической паре IV класса приложена к точке касания С звеньев 1 и 2 и направлена по общей нормали n-n (рисунок 3.4, в). Следовательно, известны направление и точка приложения этой реакции, а неизвестна ее величина.

Обозначим число подвижных звеньев плоской кинематической цепи через n, число пар V класса – через р5 и число пар IV класса – через р4.
Составим теперь условие статической определимости плоской кинематической цепи. Для каждого звена, имеющего плоскопараллельное движение, можно записать три уравнения равновесия. Если число звеньев равно n, то число уравнений – 3n. Число неизвестных реакций для пар V класса равно 2р5, а для IV класса – 1р4. Следовательно, кинематическая цепь будет статически определима, если удовлетворяется условие:
Любой механизм с парами IV классов может быть заменен механизмом с парами только V класса. Поэтому условие (3.13) примет вид:
Формула (3.14) является условием статической определимости кинематической цепи. Этому условию удовлетворяют уже известные ряды чисел звеньев и кинематических пар (см. таблицу 1.2):
| II | III | IV |
| n | ||
| р5 |
Таким образом, статически определимыми являются структурные группы Ассура. Исходя из этого, силовой расчет начинается с последней структурной группы и заканчивается расчетом ведущего звена.
3.1.4.2 Порядок проведения силового расчета
1. Выполнить структурный анализ механизма.
2. Определить скорости и ускорения всех точек звеньев механизма методом планов. Определить ускорения центров масс.
3. Определить силы тяжести. По индикаторной диаграмме (механической характеристике) определить движущую силу для соответствующего положения.
4. Определить силы инерции и моменты от сил инерции.
5. Начиная с последней от ведущего звена структурной группы, определить реакции в кинематических парах.
6. Определить уравновешивающую силу Рур из силового расчета ведущего звена.
7. Определить уравновешивающую силу 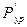
8. Определить мощность двигателя Nдв.
9. Рассчитать процент ошибки между двумя методами. Расхождение не должно составлять более 5%: Δ=(Рур— 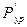
3.1.4.3 Определение реакций методом планов
Как указывалось в начале 3-ей главы, для определения реакций пользуются уравнениями равновесия твердых тел, известных из курсов «Теоретическая механика» и «Сопротивление материалов». Рассмотрим определение реакций каждой структурной группы отдельно.
Задача 1. Кинетостатический расчет структурной
группы II класса, 1 вида
Определить: R t 12, R t 43, R12, R43 – реакции во внешних шарнирах А и С; R23— реакцию во внутреннем шарнире В.


h3 
































В первую очередь определяются R t 12 и R t 43, т.к. известны их направления и точки приложения (п. 3.1.4.1). Рассмотрим 2-ое звено. Составим сумму моментов только 2-го звена относительно внутреннего шарнира (т. В):
где плечи АВ, h1, h3 – замеряются с чертежа в мм.
Рассмотрим 3-е звено. Составим сумму моментов только 3-го звена относительно внутреннего шарнира (т.В):
где плечи СВ, h2, h4 – замеряются с чертежа в мм. Тангенциальные реакции выражаются из уравнений (3.15) и (3.16). Если реакции получились отрицательные, то нужно поменять направление этих реакций.
Для определения нормальных составляющих и результирующих реакций, необходимо составить сумму сил всей структурной группы:


Это уравнение является векторным, т.е. складываются силы по правилу сложения векторов: к концу одного вектора прикладывается начало следующего. При составлении векторного уравнения необходимо учитывать, что неизвестные составляющиеставятся в начале и в концеуравнения. Прежде чем начать построение плана сил, необходимо рассчитать масштабный коэффициент сил.
Масштабным коэффициентом сил называется отношение действительного значения силы к его отрезку на чертеже:
Масштабный коэффициент сил можно рассчитать по любой известной силе или реакции. В данном случае μР рассчитан по силе инерции. Затем производится построение плана сил. На свободном поле чертежа выбирается точка полюса РР. Из нее строится вектор R t 12. К его концу прикладывается начало вектора G2, затем Ри2, Ри3, G3 и в конце R t 43 (см. уравнение 3.17 и рисунок 3.5). После построения известных сил из построения определяются неизвестные величины. Для этого из начала построения, т.е. из полюса РР, проводится линия действия реакции R n 12 || АВ и из конца построения линия действия реакции R n 43 || ВС. В точке пересечения этих линий находятся начало реакции R n 12 и конец R n 43. Результирующие реакции R12 и R43 определяются как векторные суммы нормальных и тангенциальных составляющих:

Для определения реакции во внутреннем шарнире, нужно составить векторное уравнение сил одного из звеньев, например 2-го:

и на том же плане сил необходимо соединить начало реакции R n 12 с концом Ри2. Направление этой реакции направить так, чтобы силовой многоугольник замыкался (см. рисунок 3.5).
После построения плана сил определяются действительные значения всех построенных реакций:

Задача 2. Кинетостатический расчет структурной группы
Решение. В точке А звенья 1,2 соединены во вращательную кинематическую пару, в точке В звенья 3,4 соединены в поступательную кинематическую пару. Поэтому, в точке А реакция раскладывается на нормальную и тангенциальную составляющие реакции R12, а реакция в поступательной кинематической паре R43 будет направлена перпендикулярно движению ползуна В (рисунок 3.6) и точка приложения ее неизвестна (см. п. 1.4.1).
Вначале определим величину R t 12, т.к. точка приложения и направление этой реакции известны. Для этого составим сумму моментов только 2-го звена относительно точки В

Для определения R n 12 и R43 составим сумму сил всей структурной группы

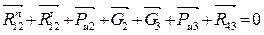
Перед построением векторного уравнения (3.22) необходимо посчитать масштабный коэффициент плана сил μР по формуле (3.18).Чертежные значения векторов сил получим, разделив действительные значения на μР. Если вектора сил получатся меньше 1 мм, то их не откладывают. Построение начинаем с известной реакции R t 12 и заканчиваем Ри3. Все вектора сил откладываем последовательно согласно уравнению (3.22), перенося их параллельно со структурной группы. Затем из начала построения, т.е. из начала вектора R t 12, проводим линию действия реакции R n 12 || АВ. После этого из конца построения, т.е. из конца силы Ри3, проводим линию действия R43 вертикально до пересечения с первой линией. Тока пересечения определит начало R t 12 и конец R43. Соединив начало R n 12 концом с R t 12, получим результирующую реакцию R12. Определим действительные значения реакций. Для этого замерим вектора на плане сил в мм и умножим их на μР:

Определим точку приложения R43, т.е. найдем расстояние hx. Для этого составим сумму моментов относительно точки А всей структурной группы:
Отложив расстояние hx параллельно движению ползуна от точки А, получим точку приложения реакции R43 (рисунок 3.6).
Более кратко остановимся на силовом расчете остальных структурных групп.
Задача 3. Кинетостатический расчет структурной группы
Исходные данные для расчета: G3 – сила тяжести в Н; РИ3 – сила инерции в Н; МРи3 – момент от силы инерции в Нм.
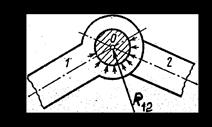
Решение. Масса кулисного камня (звена 2) не задается, т.к. система будет статически неопределимой. Поэтому реакция во внешней кинематической паре R12 будет равна реакции во внутренней кинематической паре R23 (R12=R23). Реакция R12 направлена перпендикулярно движению кулисного камня, а R23 приложена к центру шарнира (к точке А). Реакция же R43 неизвестна ни по величине, ни по направлению.
Следовательно, вначале определим R12:
Из построения плана сил определяем R43 (рисунок 3.7):


Находим действительную величину R43:
Задача 4. Кинетостатический расчет структурной группы
Исходные данные для расчета: G3 – сила тяжести в Н; РИ3 – сила инерции в Н; МРи3 = 0, МРи2 = 0 – моменты от сил инерции равны нулю, т.к. поступательные кинематические пары.
Решение. Внешние кинематические пары являются поступательными. Поэтому R12, R43 известны по направлению, а величина и точки их приложения неизвестны. Величины этих реакций определим из суммы сил всей структурной группы:


Высчитываем масштабный коэффициент μР по формуле (3.18). Строим план сил аналогично задаче 3 (рисунок 3.8) и из построения определяем неизвестные реакции.
|

Замеряем векторы полученных реакций в мм (показаны на рисунке пунктиром) и умножаем на μР:
Задача 5. Кинетостатический расчет структурной группы
Исходные данные для расчета: G3 – сила тяжести в Н; РИ3 – сила инерции в Н; МРи3 = 0, МРи2 = 0 – моменты от сил инерции равны нулю, т.к. поступательные кинематические пары.
Определить: R12, R43 – реакции во внешних кинематических парах.
Решение выполняется аналогично Задаче 4. Так как масса кулисного камня не задается, то реакция во вращательной кинематической паре R12 равна реакции в поступательной кинематической паре R32, т.е. R12 = R32.
Поэтому точка приложения и направление этих реакций известны, осталось определить величину. Строим план сил аналогично Задаче 4 (рисунок 3.9).





 |
 |








Для этого составляем уравнение плана сил:

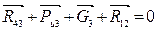
и определяем неизвестные реакции:
Таким образом, мы определили реакции для каждой структурной группы в отдельности. Теперь найдем уравновешивающую силу.