для чего нужен координатный луч
Шкалы, координаты
Для определения размера какой-либо величины (длина, вес, температура и т.д.) мы используем измерительные приборы и инструменты со шкалами для отображения результата.
Шкала – это расположенный в определенной последовательности ряд отметок, которые соответствуют числовому значению измеряемой величины.
Например, в школьном курсе математики и геометрии для измерения длины геометрического объекта, в частности отрезка, используется линейка (рисунок 1).
Рисунок 1. Измерительная линейка.
Из урока Измерение величин вы уже знаете, что такое единица измерения, а их соотношения можете посмотреть в справочном разделе.
Деления шкалы – это равные части, на которые она разбита. Каждое деление шкалы обозначается отметками (черточками).
Нулевая отметка шкалы – это отметка, которая соответствует нулевому значению измеряемой нами величины.
Цена деления шкалы – это величина значения одного деления шкалы. То есть, это величина значения между двумя соседними отметками на шкале.
Как мы видим на рисунке 1, деления, обозначенные большими черточками, пронумерованы, и значение каждого такого деления равно 1 см. В этом легко убедиться, если найти разницу между значениями каждого из соседних делений: 1-0=1, 2-1=3, …, 9-8=1, 10-9=1.
Но каждое из больших делений разделено девятью маленькими черточками на 10 делений. Мы знаем, что в 1 см содержится 10 мм, поэтому разделив эти 10 мм на 10 делений, мы получим цену деления линейки, равную 1 мм.
Цена деления может отличаться не только у разных же измерительных приборов, но и у одних и тех же.
Рисунок 2 Цена деления шкалы
Например, на рисунке 2 изображены два термометра. Как вы думаете, они показывают одинаковую температуру, или нет?
Давайте посмотрим, так ли это? На левом термометре разница между двумя соседними пронумерованными отметками равна 10°C: 10-0=10, 20-10=10, и т.д. На правом же термометре эта разница равняется уже 20°C: 20-0=20, 40-20=20, и т.д. На обоих термометрах маленькие черточки делят одно большое пронумерованное деление на 10 частей. Разделив разницу между значениями пронумерованных отметок (10 и 20 соответственно) на количество делений между ними (10), мы получим цену деления каждого из термометров:
Итак, оба термометра показывают 20°C и еще два деления. Но на левом термометре это означает 20°C и еще два раза по 1°C, то есть, 20+2=22°C, а на правом – 20°C и еще два раза по 2°C, то есть, 20+4=24°C.
Координатный луч, единичный отрезок, координаты точки
Различные прямые линии со шкалами играют важную роль в школьной математике. Сейчас я познакомлю вас с одной из них.
Нарисуем точку O и проведем от нее направо луч. Обозначим направление луча стрелкой.
Рис. 3. Луч с началом в точке O
Рис. 4. Луч с равными отрезками
Поставим возле начала луча (точки O ) число 0 (нуль). Возле второго конца отрезка OP (возле точки P ) поставим число 1 (один). Таким образом мы обозначаем, что длина отрезка OP равна 1 (единице).
Аналогичным образом вы можете легко найти числа, соответствующей каждой поставленной нами на луче точке.
Рис. 5. Луч с отрезками и цифрами
Покажу еще раз на примере точки S :
так как RS=OP (по условиям построения данных отрезков),
подставив известные нам значения длины отрезков OR и OP, получим:
Значит, точке S на нашем лучу соответствует число 3.
Оставим на луче только числовые значения, а все буквы кроме O отбросим. В итоге у нас получился вот такой луч с отрезками и числами, которые соответствуют концам этих отрезков.
Рис. 6. Координатный луч
Глядя на рисунок 6, легко заметить, что отрезки, лежащие на луче, это не что иное, как нанесенная на луч шкала. Действительно, смотрите сами.
Точка O с соответствующим ей числом 0 (нуль) называется точка отсчета, что аналогично нулевой отметке шкалы. Обычно этой буквой всегда помечают в рисунках точку отсчета.
Единичный отрезок – это отрезок, длина которого принята нами за единицу длины и равна 1(единице). Точке, обозначающей правый конец единичного отрезка, соответствует число 1.
Координатный луч – это луч с отмеченным на нем единичным отрезком, точкой начала отсчета, которой соответствует число 0 (нуль), и указанным направлением отсчета.
Координатный луч еще называют числовой луч.
Координатный луч — это не что иное, как бесконечная шкала.
Длина единичного отрезка может быть любой. Она выбирается каждый раз отдельно и при ее выборе ориентируются на то, чтобы на рисунке поместились все необходимые в данный момент числа. Например, на рисунке 7-а длина единичного отрезка составляет 5 см, а на рисунке 7-б всего 1 см.
Рис. 7. Разные варианты единичного отрезка
Как вы заметили из предыдущего рисунка, для разметки луча отрезками можно вместо кружочков использовать штрихи везде, кроме точки O (начала отсчета). Кружочки рисуют поверх этих штрихов тогда, когда необходимо отметить на числовом луче какое-то натуральное число. В этом случае мы дополнительно обозначаем его заглавной (большой) буквой латинского алфавита (смотрите рисунок 8).
Координатный луч служит для наглядного отображения и сравнения чисел натурального ряда.
Действительно, длина каждого отрезка числового луча отличается от длины предыдущего на единицу, точно так же, как и каждый элемент числового ряда отличается от предыдущего.
Координата точки числового луча – это число, которое соответствует поставленной на числовом луче точке.
Рис. 8. Координаты точек
Точке A соответствует число 5 координатного луча, точке B – число 8, точке C – число 13. Запишем полученные координаты точек: A ( 5 ), B ( 8 ), C ( 13 ).
В отдельных случаях для обозначения на координатном луче больших натуральных чисел, допускается не отображать на рисунке точку отсчета и единичный отрезок, показывая только тот участок луча, на котором расположены данные числа.
Рис. 9. Большие числа на координатном луче.
Насколько публикация полезна?
Нажмите на звезду, чтобы оценить!
Средняя оценка 4.2 / 5. Количество оценок: 9
Урок 7 Бесплатно Координатный луч
Ответим на вопрос, почему луч подходит больше всего для обозначения натуральных чисел, а также научимся определять с помощью него длины отрезков.
Определение
Луч- это часть прямой ограниченная с одной стороны точкой, называемой началом луча.
Начертим луч с началом в точке О так, чтобы он шел слева направо, и отметим на нем точку А не очень далеко от начала.
Отрезок ОА назовем единичным отрезком.
Далее отложим от точки А следующий отрезок АВ, равный отрезку ОА.
Затем отложим от точки В отрезок ВС, также равный единичному отрезку.
Продолжим процесс, уже не называя точки.
Так мы получили шкалу, которую называют координатным лучом.
В самом деле, для шкалы нам необходимы были такие объекты, как штрих, деление, цена деления, посмотрим, чем они представлены в данном случае.
В роли штрихов выступают точки.
Изображая координатный луч, можно точки обозначать как небольшие штрихи, это ничуть не делает рисунок менее точным.
Делением в данном случае является отрезок между любыми соседними точками.
Этот отрезок всегда равен единичному по построению, ведь мы всегда откладывали отрезок, равный единичному.
Ценой деления в данном случае является единица.
Может быть немного непривычно, что единица идет без наименования, ведь на других шкалах обычно цена деления 1 кг, 1 см, 1 км/ч.
Но здесь идет измерение натуральных чисел, поэтому просто единица.
Так что координатный луч вполне можно считать шкалой.
Если же говорить про более конкретное определение, то вот оно.
Нередко к этому определению добавляют помимо единичного отрезка еще два объекта: точку начала отсчета и направление увеличения чисел.
А на координатном луче точка начала отсчета и точка начала луча всегда совпадают.
Направление задавать тоже нет необходимости, ведь у луча только одно вполне определенное направление: от начала.
Единичный отрезок же необходим, ведь без него не будет одинакового расстояния между соседними точками и смысла в луче не будет.
Отметим важный момент: в одном координатном луче всегда один единичный отрезок.
Пройти тест и получить оценку можно после входа или регистрации
Координаты
Мы уже поговорили про координатный луч, но важно понять, почему он “координатный” и как определены координаты в данном случае.
Обычно можно услышать слово “координаты” в географическом контексте.
Когда мы узнаем координаты, а это два числа, то можем однозначно сказать, про какую точку на карте идет речь.
Другими словами, в географическом смысле, координаты являются числами, определяющими положение точки на карте.
В случае с координатным лучом все даже проще.
Координата точки на координатном луче соответствует количеству единичных отрезков между этой точкой и точкой начала отсчета.
Посмотрим еще раз на рисунок из прошлой главы:
Точка А находится на расстоянии одного единичного отрезка от точки начала отсчета.
Точке А соответствует число 1
Точка В находится на расстоянии двух единичных отрезков от точки начала отсчета.
И точке В соответствует число 2
Аналогично каждой следующей точке соответствует число на единицу больше.
Число, соответствующее точке на координатном луче, называют координатой этой точки.
Заметим теперь, как соответствуют друг другу натуральный ряд и координатный луч.
За исключением точки начала отсчета, каждой точке соответствует натуральное число.
Если смотреть от начала отсчета, то координата следующей точки после данной равна следующему натуральному числу после координаты данной точки.
И также мы знаем, что координата точки P равняется 276
Тогда мы сможем сказать координату точки Q, это будет следующее натуральное число после числа 276, то есть ответ: 277
Аналогичная логика работает и в другую сторону.
Координата точки, идущей перед данной, является предыдущим натуральным числом по отношению к координате данной точки.
Допустим, точки E и R соседние.
Также известно, что R находится дальше от точки начала отсчета, чем Е; а также известна координата точки R, она равна 315
Чтобы найти координату точки Е достаточно взять предыдущее натуральное число от числа 315, это будет число 314
Эти примеры показывают, как натуральный ряд ложится на координатный луч.
Отметим, что именно луч идеально соответствует натуральным числам, ведь и луч, и натуральный ряд ограничены с одной стороны (с начала), но продолжаются бесконечно.
Если же нам надо найти координату точки безотносительно соседних точек, то достаточно отсчитать количество единичных отрезков между данной точкой и точкой начала отсчета.
Найдем координату точки Н.
Между ей и точкой О (началом отсчета) 4 единичных отрезка, значит, координата точки Н равна 4
Пройти тест и получить оценку можно после входа или регистрации
Координатный луч

Всего получено оценок: 413.
Всего получено оценок: 413.
Координатный луч – это одна из систем ориентации в плоскости и сравнения чисел. Координатный луч очень часто используется при решении задач. Имеет смысл поговорить о координатном луче, выделить его особенности и отличия, определить правильную область применения.
Что такое координатный луч?
Координатный луч – это один из способов ориентации на плоскости.
Любой координатный луч имеет:
Направление движения обычно указывает сторону увеличения показателей.
Координатный луч позволяет определить положение точки только вдоль прямой. Что это значит? Представим себе координатный луч в виде реки. Так вот, мы можем определить положение путника у реки, но при этом, насколько он ушел вглубь берега – мы понять не сможем.
Поэтому чаще всего, вместо координатной прямой, используется декартова системы координат.
Когда-то мореплаватели к системе координатной прямой добавили угол, на который поднимается точка над линией горизонта. Так появилась полярная система координат. Это одна из самых древних систем навигации в мире.
Но координатную прямую удобно использовать для чертежей при решении задач, поэтому она до сих пор используется в курсе математики.
Чем отличается координатный луч от координатной прямой?
До этого мы уже говорили о координатной прямой. Следует сразу разделить координатный луч, числовой луч и координатную прямой.
Координатный и числовой лучи очень схожи. Различие заключается в том, что числовой луч может начинаться с любой точки и эта точка будет его началом. Все зависит от чисел, которые нам требуется сравнить. Координатный луч начинается всегда с 0, иначе он не может считаться координатным.
Координатная прямая же, в отличие от координатного луча, может быть продлена как в право, так и в лево от начала координат. Это позволяет отмечать на координатной прямой отрицательные числа.
Для того чтобы отметить отрицательные координаты на координатном луче, придется построить другой луч, который будет направлен влево.
Область применения
На самом деле, область применения координатного луча достаточно мала. Это могут быть:
На самом деле, это одна из гениальных идей математики: соединить вместе 4 координатных луча для получения системы ориентации на плоскости. Два луча лежат на одной прямой и направлены в противоположные стороны, при этом два других луча лежат на прямой, перпендикулярной первой и так же направлены в противоположные стороны.
В результате получилась система, которую уже несколько сотен лет применяют для ориентирования на плоскости. Более того, декартову систему можно перевести в пространство.
Эту систему навигации используют спутниковые системы, радары, навигационные системы автомобилей. Такой системой пользуются художники при использовании компьютерной графики. И всему этому положил начало координатный луч. Поэтому нельзя сказать, что он бесполезен. Просто луч имеет малую область применения, но именно он положил начал современным системам навигации.
Что мы узнали?
Мы поговорили об определении координатного луча. Выделили его отличия от числового луча и координатной прямой. Оговорили область применения и особенности координатного луча в математике 5 класса.
Координатная прямая (числовая прямая), координатный луч
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.
Координатный луч
Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.
На примере мы видим, что O является началом луча.
Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.
От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.
Координатный луч – это шкала, которая может длиться до бесконечности.
Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.
Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.
Координатная прямая
Проведите луч в противоположную сторону, дополнив его до прямой
Отложите единичные отрезки по примеру, указанному выше
Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.
Соответствие между точками координатной прямой и действительными числами
Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.
Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.
Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.
Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.
Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.
Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.
Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.
Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.
Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.
Благодаря этому утверждению координатную прямую зачастую определяют как числовую.
Координаты точек на координатной прямой
Число, соответствующее точке на координатной прямой, называется координатой этой точки.
Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.
Для чего нужен координатный луч
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
В этом уроке Вы научитесь строить координатный луч, а также определять координаты точек, расположенных на нем.
Чтобы построить координатный луч, нам сначала потребуется, конечно же, сам луч.
Обозначим его OX, точка O – начало луча.
Забегая вперед, скажем, что точку O называют началом отсчета координатного луча.
Луч можно изображать в любом направлении, однако во многих случаях луч проводят горизонтально и вправо от его начала.
Итак, начертим луч ОХ горизонтально слева направо и обозначим его направление стрелкой. Отметим на луче точку Е.
Над началом луча (точкой О) напишем 0, над точкой Е – цифру 1.
Отрезок ОЕ называют единичным.
Далее на луче отложим отрезок ЕА, равный единичному отрезку, и над точкой А напишем цифру 2.
Так, шаг за шагом, откладывая единичные отрезки, получим бесконечную шкалу.
Числа 0, 1, 2 называют координатами точек О, Е и А. Пишут точка О и в скобках указывают ее координату ноль – О(о), точка Е и в скобках ее координата один – Е(1), точка А и в скобках ее координата два – А(2).
Таким образом, для построения координатного луча необходимо:
1. начертить луч ОХ горизонтально слева направо и обозначить его направление стрелкой, над точкой O написать число 0;
2. нужно задать так называемый единичный отрезок. Для этого на луче нужно отметить какую-нибудь точку, отличную от точки O (на этом месте принято ставить не точку, а штрих), и над штрихом записать число 1;
3. на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному и тоже поставить штрих, далее от конца уже этого отрезка нужно отложить еще один единичный отрезок, также отметить штрихом и так далее;
4. чтобы координатный луч принял законченный вид, осталось записать над штрихами слева направо числа из натурального ряда чисел: 2, 3, 4, и так далее.
Давайте выполним задание:
На координатном луче нужно отметить следующие точки: точку М с координатой 1, точку Р с координатой 3 и точку А с координатой 7.
Точка М будет расположена правее нуля на две клетки, точка Р будет расположена правее нуля на 6 клеток, так как 3 умножить на 2, будет 6, и точка А – правее нуля на 14 клеток, так как 7 умножить на 2, получится 14.
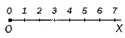
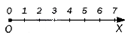
Найдите и запишите координаты точек А; В; и С отмеченных на данном координатном луче
Данный координатный луч имеет единичный отрезок, равный одной клетке, значит координата точки А равна 4, координата точки В равна 8, координата точки С равна 12.
Подведем итог, луч ОХ с началом отсчета в точке О, на котором указаны единичный отрезок и направление, называют координатным лучом. Координатный луч представляет собой не что иное, как бесконечную шкалу.
Число, которое соответствует точке координатного луча, называется координатой этой точки.
Например: А и в скобках 3.
Читают: точка А с координатой 3.
Следует заметить, что очень часто координатный луч изображают лучом с началом в точке O, и откладывают от его начала единственный единичный отрезок, над концами которого записывают числа 0 и 1. В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.
Таким образом, в этом уроке Вы научились строить координатный луч, а также определять координаты точек, расположенных на координатном луче.