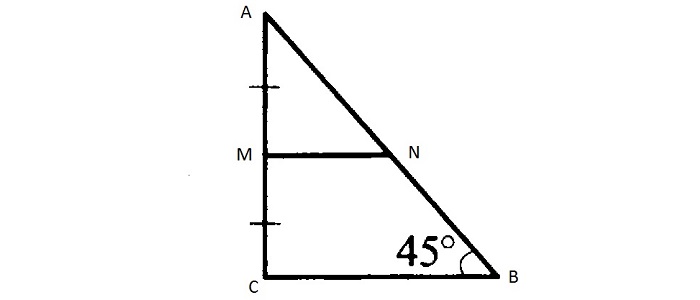
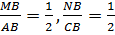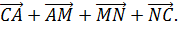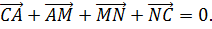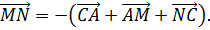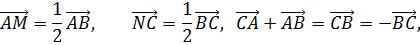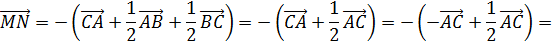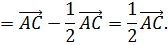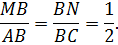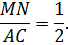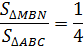для чего используются средние линии
Применение средней линии треугольника к решению задач. Теорема Вариньона
Класс: 8
Ключевые слова: профильный уровень
Презентация к уроку
Класс: 8 класс.
Тип урока: изучение нового материала.
Цели урока:
Задачи урока:
Методы обучения: проблемно-поисковый.
Содержание деятельности: моделирование ситуации, в которой у учащихся возникает потребность в расширении запаса знаний.
Форма организации урока: индивидуальная, фронтальная.
Оборудование урока: доска, проектор, дидактический материал (тексты задач) на каждого ученика.
Учитель готовит на доске:
Этапы урока:
Организационный момент
Учитель сообщает тему урока и цели урока.
Учитель: Сегодня на уроке мы продолжим знакомство свойством средней линии треугольника. Разберем некоторые задачи, решаемые с помощью этого свойства.
Актуализация знаний
Разбор задачи №1 из домашнего задания.
Задача №1.
Доказательство:
Наводящие вопросы
Учитель: Что можно сказать об отрезках ЕТ и РК?
Учитель: Каким свойством обладает средняя линия треугольника?
Новый материал
Учитель: Ребята, начертите произвольный четырехугольник (один ученик приглашается для работы у доски). Отметьте середины сторон и последовательно их соедините. Как вы думаете какая геометрическая фигура получилась?
Учащиеся выдвигают гипотезы: 1) четырехугольник; 2) параллелограмм.
Учитель: Ребята, давайте докажем следующее утверждение.
Утверждение. Доказать, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.
Доказательство проходит в виде беседы.
Доказательство:
Учащиеся последовательно соединяют середины сторон четырехугольника.
Учащимся рассмотреть пару противоположных отрезков. Учащиеся отмечают сходство с домашней задачей №1. Предлагают провести диагональ четырехугольника так, чтобы получилось два треугольника со средними линиями. Проводят доказательство.
Учитель: Ребята, данное утверждение называется ТЕОРЕМОЙ ВАРИНЬОНА.
Тема урока: Теорема Вариньона.
Тренировочные упражнения (12 мин.)
Учитель: Ребята, как будет выглядеть доказательство домашней задачи №1, если применить теорему Вариньона? (Обговорить устно).
Учащиеся отмечают, насколько быстро можно решить задачу, используя теорему Вариньона.
Учитель: Молодцы. А теперь мы рассмотрим задачи на применение теоремы Вариньона. Учащиеся работают в парах. Предлагают свои решения (документ камера).
Правильное решение оформляется на доске.
Задача № 1. Отрезки, соединяющие середины противоположных сторон четырёхугольника, равны. Докажите, что диагонали четырёхугольника перпендикулярны.
Доказать, что АС ┴ ВD.
Задача № 2*. Середины сторон AB и CD, BC и ED выпуклого пятиугольника ABCDE соединены отрезками. Точки H и K соответственно – середины этих отрезков.
Доказать, что отрезок HK параллелен стороне AE и равен одной четверти этой стороны.
Указания. Рассмотреть четырехугольник ABCD и воспользоваться теоремой Вариньона. Рассмотреть среднюю линию треугольника ADE.
Итог урока
Учитель: Что нового вы сегодня узнали на уроке?
Ученик: Сформулировали и доказали теорему Вариньона. Решали задачи, используя данную теорему.
Учитель просит учащихся сформулировать теорему Вариньона.
Учитель: Молодцы. Урок окончен, до новых встреч.
Что такое средняя линия треугольника
В данной публикации мы рассмотрим определение, свойства и признак средней линии треугольника, а также разберем пример решения задачи для лучшего понимания теоретического материала.
Определение средней линии треугольника
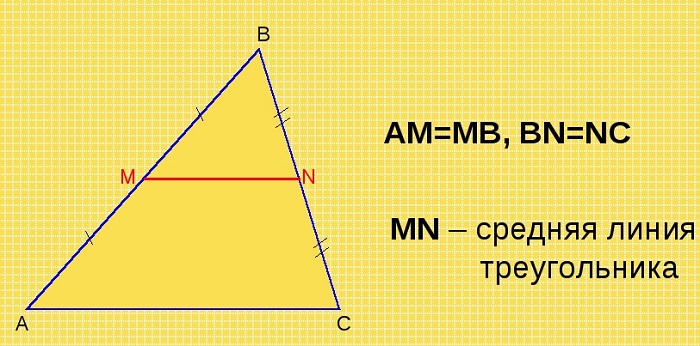
Отрезок, который соединяет середины двух сторон треугольника, называется его средней линией.
Свойства средней линии треугольника
Свойство 1
Средняя линия треугольника параллельна одной из его сторон (которую не пересекает) и в два раза меньше этой стороны.
Свойство 2
Средняя линия треугольника отсекает от него подобный треугольник (в соотношении 1:2), площадь которого в 4 раза меньше исходного.
Свойство 3
В любом треугольнике можно провести три средние линии.
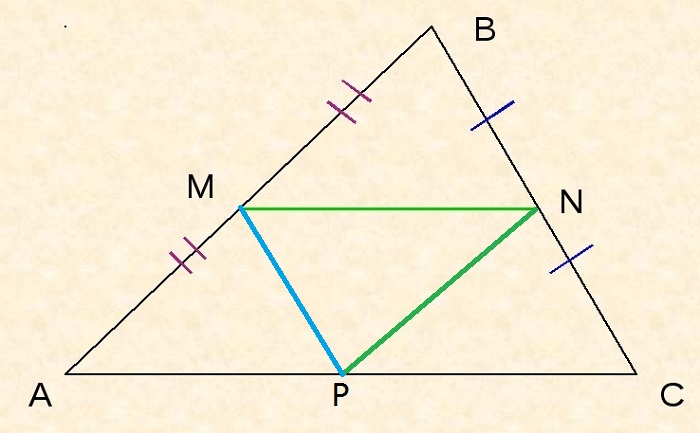
KL, KM и ML – средние линии треугольника ABC.
Свойство 4
Три средние линии треугольника делят его на 4 равных по площади треугольника.
Признак средней линии треугольника
Отрезок, проходящий через середину одной из сторон треугольника, пресекающий вторую и параллельный третьей стороне, является средней линией этого треугольника.
Пример задачи
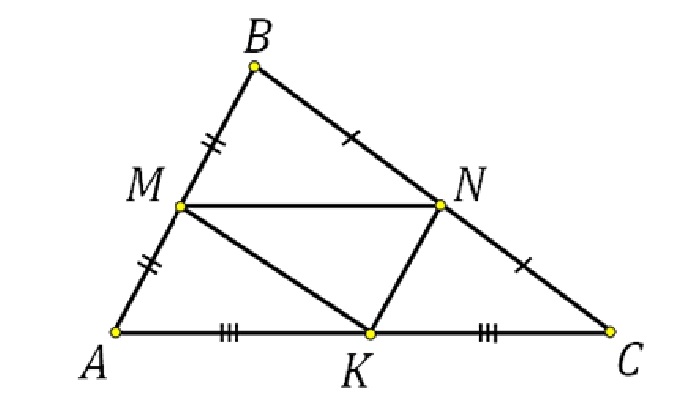
Дан треугольник, две стороны которого равны 6 и 8 см. Найдите длину средней линии, соединяющей эти стороны.
Треугольник с заданными сторонами является прямоугольным, причем известные значения – это длины катетов. Средняя линия, которая соединяет катеты, параллельна гипотенузе и равна половине ее длины.
Мы можем найти гипотенузу, воспользовавшись теоремой Пифагора.
BC 2 = AB 2 + AC 2 = 6 2 + 8 2 = 100.
BC = 10.
Таким образом, средняя линия LM = 1 /2 ⋅ BC = 1 /2 ⋅ 10 = 5.
Одним из важных понятий, с помощью которого легко решается целый класс задач по геометрии, является средняя линия треугольника.
Разберём данное понятие, рассмотрим свойства, и научимся правильно решать задачи на эту тему.
Определение и признаки средней линии треугольника
Отрезок, соединяющий середины двух сторон треугольника, называется его средней линией.
Отрезок, у которого один из концов совпадает с серединой одной из сторон, другой находится на второй стороне, проведённый параллельно третьей стороне, является средней линией треугольника.
Доказательство следует из теоремы Фалеса.
Теорема о средней линии треугольника
Средняя линия треугольника параллельна основанию (третьей стороне) и равна её половине.
Существует три вида доказательств этого положения. Каждое из них базируется на одной из ключевых позиций планиметрии.
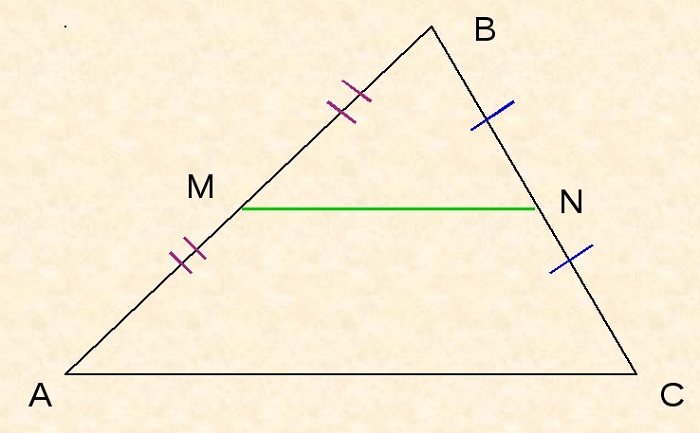
Пусть дан треугольник ABC, M – середина стороны AB, N – середина BC.
По определению, MN – средняя линия ΔABC.
Необходимо доказать, что MN II AC, MN = ½AC.
Доказательства
Пусть прямая MK II AC. Тогда по теореме Фалеса MK пересекает сторону BC в её середине. В этом случае отрезок MN лежит на прямой MK.
Следовательно, MN II AC.
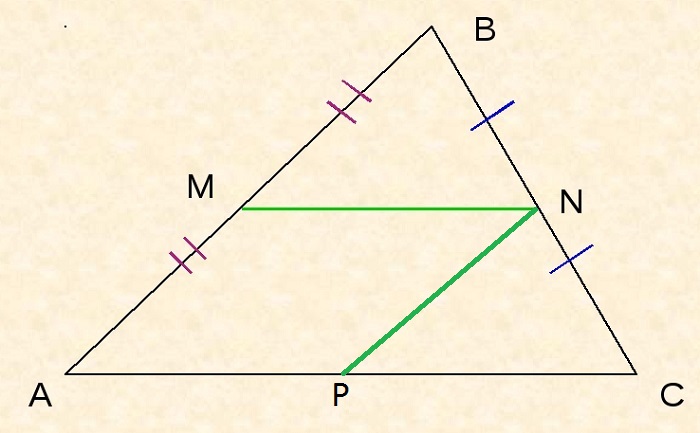
Тогда NP – средняя линия по теореме Фалеса, то есть AP = PC.
Так как AMNP – параллелограмм по определению, то AP = MN. Из этого и предыдущего утверждения следует, что длина MN равна ½AC.
Рассматриваются треугольники MBN и ABC. В них угол B является общим,
По второму признаку подобия треугольников ΔMBN ∼ ΔABC. Следовательно, углы BMN и BAC равны.
Поскольку эти углы являются соответственными, то прямые MN и AC параллельны.
Формула MN = ½AC следует из условий
поскольку пропорциональность двух пар сторон влечёт соответствующее отношение для третьей пары сторон.
Рассматривается сумма векторов
Поскольку в результате образуется замкнутая ломаная, то
Отсюда следует, что
Из последнего равенства следуют условия теоремы.
Следствия из теоремы с доказательствами
Следствие №1
Средняя линия отсекает треугольник, подобный данному, с коэффициентом подобия ½ и площадью, составляющий ¼ площади заданного треугольника.
По определению стороны AB и BC делятся пополам, поэтому
Из третьего признака подобия вытекает рассматриваемое свойство.
Поскольку площади подобных фигур относятся как квадрат коэффициента подобия, то получается вторая часть свойства, то есть площадь маленького треугольника относится к площади большого как
Следствие №2
Поскольку MN – средняя линия, то MN II AC, поэтому ∠BMN = ∠BAP, ∠BNM = ∠BCA как соответственные при MN II AC и секущей AB или BC соответственно.
Поскольку MP – средняя линия, то MP II BC, поэтому ∠MPA = ∠BCA как соответственные при MP II BC и секущей AC.
Таким образом: ∠BNM = ∠BCA = ∠MPA.
Так как MN – средняя линия, то сторона MN = ½AC, поэтому MN = AP.
Следовательно, ΔAMP = ΔMBN по второму признаку равенства треугольников.
Равенство остальных пар треугольников доказывается аналогично.
По основному свойству ΔMBN ∼ ΔABC с коэффициентом подобия ½. Так как все полученные маленькие треугольники равны между собой, то каждый из них, следовательно, подобен большому с тем же коэффициентом.
Свойства средней линии треугольника
Теорема и следствия из неё составляют основные свойства средней линии треугольника.
Согласно второму утверждению, вид большого треугольника такой же, как и у маленьких. То есть для равностороннего и равнобедренного треугольников средние линии отсекают равносторонние и равнобедренные треугольники.
Высоты тупоугольного треугольника, проведённые к тупому углу из вершин острых, располагаются вне треугольника. Поэтому часто рассматривают не саму среднюю линию, а её продолжение. Учитывая подобие получаемых фигур, можно утверждать, что точкой пересечения с продолжением средней линии высота делится на две равные части.
Биссектриса угла треугольника точкой пересечения со средней линией также делится пополам.
Средняя линия прямоугольного треугольника
Для прямоугольного треугольника две средние линии перпендикулярны катетам, а третья равна медиане, проведённой к гипотенузе.
Остроугольный разносторонний треугольник не имеет средних линий, обладающих подобными характеристиками.
Пример решения задачи
Доказать, что середины сторон произвольного выпуклого четырёхугольника являются вершинами параллелограмма.
Проводя диагональ четырёхугольника, получают разбиение на два треугольника, в каждом из которых построена средняя линия, параллельная по основной теореме диагонали, как основанию.
Так как две прямые, параллельные третьей, параллельны между собой, то противолежащие стороны образованного средними линиями четырёхугольника параллельны.
Аналогично доказывается параллельность двух других сторон нового четырёхугольника. По определению четырёхугольник, полученный соединением середин сторон заданного четырёхугольника, является параллелограммом.
Типы линий на чертеже и их назначение по ГОСТу
Ни один чертеж не имеет смысла, если в нем отсутствуют специальные линии. Они являются основным элементом, с помощью которого специалисты успешно читают и понимают чертеж.
Какие бывают линии, зачем они нужны и что по этому поводу говорит ГОСТ — в этой статье.
Что представляют собой линии и ГОСТ
Чтение чертежа существенно облегчается и становится проще, когда используют различные варианты линий — у них различные вид и назначение. Все эти варианты установлены и регламентируются ГОСТами.
Один из них — ГОСТ 2.303-68 о Единой системе конструкторской документации.
ГОСТ считается основным: его используют преподавательский состав и инженеры, работа которых непосредственно связана с созданием чертежей. Он же лег в основу более усовершенствованного стандарта 2.109-73.
На первом этапе черчения нужно использовать сплошные тонкие линии. Только после уточнения формы, габаритов, размещения картинки, удаления дополнительных линий, берут вспомогательные линии, предписанные стандартом.
Какие типы линий применяются в чертежах
Выделяют 7 основных типов линий для создания чертежей:
Параметр толщины толстой сплошной линии — ориентир для других. Но есть один нюанс: каждый тип линий по всему чертежу прочерчивается с одинаковой толщиной.
Важно, чтобы осевые и центровые линии выходили за пределы контура картинки на 2-5 мм и в конце была не точка, а штрих.
Наименование
Начертание
Сплошная толстая линия







Сплошная тонкая с изломами

Штрихпунктирная с двумя точками тонкая

Наименование
Толщина линии по отношению к толщине основной линии
Основное назначение
Сплошная толстая линия
Сплошная тонкая с изломами
Длинные линии обрыва
Штрихпунктирная с двумя точками тонкая
Последовательность черчения линий
Разработана специальная инструкция, определяющая последовательность отображения линий.
Первый этап — подготовка листа, в которую входит оформление рамки и разметка мест будущих участков детали.
Второй этап — прочерчивание центровых и осевых линий. Начинают процесс черчения с горизонтальных отрезков.
Третий этап — отображение окружностей и дуг радиусов. Вначале — меньшие.
Четвертый этап — последовательное проведение линий: горизонтальных, вертикальный, наклонных.
Пятый этап — обозначение участков детали с помощью специальных линий.
После этого готовый эскиз можно прорисовывать чернилами.
Как прорисовываются линии на чертеже
Выверенный алгоритм прорисовки делает изображение четче и позволяет добиться правильных пропорций толщины линий.
Средняя линия
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон этой фигуры. Понятие употребляется для следующих фигур: треугольник, четырехугольник, трапеция.
Содержание
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника. [1]
Свойства
Средняя линия четырехугольника
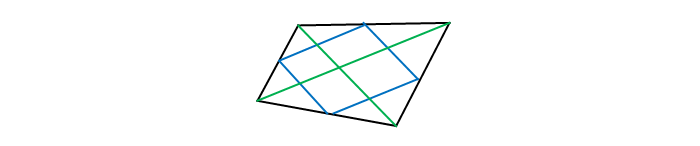
Средняя линия четырехугольника — отрезок, соединяющий середины противолежащих сторон четырехугольника.
Свойства
Первая линия соединяет 2 противоположные стороны. Вторая соединяет 2 другие противоположные стороны. Третья соединяет центры двух диагоналей ( не во всех четырехугольниках центры пересекаются)
Средняя линия трапеции
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Свойства
См. также
Примечания
Полезное
Смотреть что такое «Средняя линия» в других словарях:
СРЕДНЯЯ ЛИНИЯ — (1) трапеции отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции параллельна её основаниям и равна их полусумме; (2) треугольника отрезок, соединяющий середины двух сторон этого треугольника: третья сторона при этом… … Большая политехническая энциклопедия
СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции) отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Большой Энциклопедический словарь
средняя линия — 24 средняя линия: Воображаемая линия, проходящая через профиль резьбы так, что толщина выступа равна ширине канавки. Источник … Словарь-справочник терминов нормативно-технической документации
средняя линия — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции). * * * СРЕДНЯЯ ЛИНИЯ СРЕДНЯЯ ЛИНИЯ треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Энциклопедический словарь
средняя линия — vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis 3 mm linija, dalijanti teniso stalo paviršių išilgai pusiau. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas
средняя линия — vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis Linija, dalijanti fechtavimosi kovos takelį į dvi lygias dalis. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas
средняя линия — vidurio linija statusas T sritis Kūno kultūra ir sportas apibrėžtis Linija, dalijanti sporto aikšt(el)ę pusiau. atitikmenys: angl. centre line; midtrack line vok. Mittellinie, f rus. средняя линия … Sporto terminų žodynas
Средняя линия — 1) С. л. треугольника, отрезок, соединяющий середины двух сторон треугольника (третью сторону называют основанием). С. л. треугольника параллельна основанию и равна его половине; площади частей треугольника, на которые делит его с. л.,… … Большая советская энциклопедия
СРЕДНЯЯ ЛИНИЯ — треугольника отрезок, соединяющий середины двух сторон треугольника. Третья сторона треугольника при этом наз. основанием треугольника. С. л. треугольника параллельна основанию и равна половине его длины. Во всяком треугольнике С. л. отсекает от… … Математическая энциклопедия
СРЕДНЯЯ ЛИНИЯ — треугольника (трапеции), отрезок, соединяющий середины двух сторон треугольника (боковых сторон трапеции) … Естествознание. Энциклопедический словарь